Algebra
Category : 6th Class
Algebra
Learning Objectives
Algebra
Algebra is generalized arithmetic in which unknown or unspecified numbers are represented by using letters known as literals.
Constant and variable: A symbol having a fixed numerical value is called a constant and a symbol which takes on various numerical values is known as variables.,
Example: \[8,-25,\text{ }6\frac{6}{11},\,3\frac{1}{2}\] are examples of constants whereas a, b, c, u, u x and y are examples of variables.
Algebraic expression: An algebraic expression composed of arithmetic numbers, letters and signs of operation.
Example: \[5x+8,\text{ }9y+3x\] and 8z are examples of algebraic expressions.
Terms of an expression: Various parts of an algebraic expression separated by the signs plus (+) or minus (-) are known as the terms of the expression.
Example: The algebraic expression \[6x+8y+9\] have three terms, 6x, 8y and 9.
Monomial: An algebraic expression having only one term is known as monomial.
Example: \[2,5x,6xy\] and\[-89xyz\] are examples of monomials.
Binomial: An algebraic expression having two terms is known as binomial.
Example: \[2x+y,3z+5y\] and \[x+8\]are examples of binomials,
Trinomial: An algebraic expression having three terms is known as trinomial
Example: \[x+y-9,\text{ }5a+6b+c\] and \[5x+xy+9\] are examples of trinomials.
Polynomial: An algebraic expression containing two or more terms is called polynomial,
Example: \[5x+6,\text{ }7x+8y+9\]and \[15+xy+9y+8x\] are examples of polynomials,
Factor: A factor is any one of two or more numbers that are multiplied together.
Example: 5 and x are factors of 5x.
Coefficients: In a product of numbers and literals, any of the factors is called the coefficient of the product of other factors.
Example: In 7xy, the coefficient of x is 7y and the coefficient of y is 7x.
Like terms: The terms which have the same literal factors are called like or similar terms.
Example: 7x, 9x, x are examples of like terms.
Unlike terms: The terms which have different literal factors are called unlike or dissimilar terms.
Example: \[5x,3xy,7xz\] are examples of unlike terms.
Algebraic equation: An equation is a mathematical statement equating two quantities.
Example: \[x+9=15,\text{ }5x-8=3x\] and \[3x-7=4\] are examples of algebraic equations.
Solution of equation: The value of the variable in an equation which satisfies the equation is called solution of the equation.
Example: \[x+9=20\], here the value \[~x=11\] satisfies the equation/ therefore \[~x=11\] is the solution of the equation \[x+9=20\].
Ratio
The ratio of two quantities of the same kind and in the same units is a fraction which shows how many times the one quantity is of other.
Example
If a and b are two physical quantities of same kind and in the same units, then the fraction \[\frac{a}{b}\]is called the ratio of a to b and denoted as a : b. Here a and b are called terms of the ratio.
The former 'a' is called the first term or antecedent and the latter b is called second term of consequent
Note 1: A ratio is unchanged if the two numbers of the ratio are multiplied or divided by the same number.
Note 2: The order of the terms in a ratio is very important. If order of terms is changed then the ratio of the quantities will also changed. For example 2 : 3 and 3 : 2 are two different ratios.
Ratio in the simplest form: The ratio a : b is said to be in the simplest form if a and b have no common factor other than 1.
Proportion
A proportion is an equation that states that two ratios are equal. In other words four numbers a, b, c, and d are said to be in proportion if the ratio a : b is equal to the ratio c: d and the proportion is written as a : b :: c : d.
Example
Consider the two ratio 6: 8 and 12 : 16. Simplest form of the ratio 6 : 8 is 3 :4 and also simplest form of the ratios 12 : 16 is 3 : 4, therefore, the ratios 6 : 8 and 12 :16 are equal. Thus, 6 : 8 :: 12 : 16 is a proportion.
Terms of the proportion: In the proportion \[a:b::c:d,a,b,c\] and d are called first, second, third and fourth terms of the proportion, respectively. First and fourth term of the proportion are called extreme terms whereas second and third terms are called middle terms.
A relation between the terms: Product of extreme terms = product of middle terms.
Continued proportion: Three numbers a, b and c are said to be in continued proportion if a, b, b, c are in proportion.
Mean proportional: If a, b c are in continued proportion then b is known as the mean proportional between a and c.
Third proportional: If a, b, c are in continued proportion then c is called the third proportional.
Commonly Asked Questions
Add the following polynomials \[{{\mathbf{x}}^{\mathbf{3}}}\mathbf{-3}{{\mathbf{x}}^{\mathbf{2}}}\mathbf{-6x+10}\] and \[\mathbf{4}{{\mathbf{X}}^{\mathbf{3}}}+\mathbf{10}{{\mathbf{X}}^{\mathbf{2}}}+\mathbf{15X}-\mathbf{20}\]?
(a) \[5{{X}^{3}}+7{{X}^{2}}+9X-10\]
(b) \[5{{X}^{2}}+6+45\]
(c) \[5x-3{{x}^{2}}+6\]
(d) All of these
(e) None of these
Answer (a)
\[{{x}^{3}}-3{{x}^{2}}-6x+10\]
Explanation:
![]()
Alternative Method
\[({{X}^{3}}-3{{X}^{2}}-6X+10+\left( 4{{X}^{3}}+10{{X}^{2}}+15X-20 \right)\]
\[{{X}^{3}}-3{{X}^{2}}-6X+10+4{{X}^{3}}+10{{X}^{2}}+15X-20\]
\[={{X}^{3}}+4{{X}^{3}}-3{{X}^{2}}+10{{X}^{2}}-6X+15X+10-20\]
\[=5{{X}^{3}}+7{{X}^{2}}+9X-10.\]
Subtract: \[\mathbf{4}{{\mathbf{X}}^{\mathbf{2}}}\mathbf{Y}-\mathbf{3XY}+\mathbf{5X}\] from \[\mathbf{10}{{\mathbf{X}}^{\mathbf{2}}}\mathbf{Y-6XY+15X-25?}\]
(a) \[8{{X}^{3}}+2{{X}^{2}}+9X\] (b) \[6{{X}^{2}}Y-3XY+10X-25\]
(c) \[5X-3{{X}^{2}}+6\]
(d) \[6{{X}^{2}}Y-2XY+12X-5\]
(e) None of these
Answer: (b)
Explanation:
\[=(10X-6XY+15X-25)-(4{{X}^{2}}Y-3XY+5X)\]
\[=10{{X}^{2}}-6XY+15X-25-4{{X}^{2}}Y+3XY-5X\]
\[=10{{X}^{2}}Y-4{{X}^{2}}Y-6XY+3XY+15X-5X-25\]
\[=6{{X}^{2}}Y-3XY+10X-25.\]
Multiply, \[\mathbf{(}{{\mathbf{a}}^{\mathbf{2}}}\mathbf{+ab+}{{\mathbf{b}}^{\mathbf{2}}}\mathbf{)(}{{\mathbf{a}}^{\mathbf{2}}}\mathbf{-ab-}{{\mathbf{b}}^{\mathbf{2}}}\mathbf{)}\]
(a) \[{{a}^{4}}-{{a}^{2}}{{b}^{2}}-2a{{b}^{3}}-{{b}^{4}}\]
(b) \[6{{a}^{2}}b-3ab+10a-25\]
(c) \[5a-3{{a}^{2}}+6\]
(d) All of these
(e) None of these
Answer (a)
Explanation: \[({{a}^{2}}+ab+{{b}^{2}})({{a}^{2}}-ab-{{b}^{2}})\]
\[={{a}^{2}}({{a}^{2}}-ab-{{b}^{2}})+ab({{a}^{2}}-ab-{{b}^{2}})+{{b}^{2}}({{a}^{2}}-ab-{{b}^{2}})\]
\[={{a}^{4}}-{{a}^{3}}^{~}b-{{a}^{2}}{{b}^{2}}+{{a}^{3}}b-{{a}^{2}}{{b}^{2}}-a{{b}^{3}}+{{a}^{2}}{{b}^{2}}-a{{b}^{3}}-{{b}^{4}}\]
\[={{a}^{4}}-{{a}^{2}}^{~}{{b}^{2}}-a{{b}^{3}}-a{{b}^{3}}-{{b}^{4}}\]
\[={{a}^{4}}-{{a}^{2}}^{~}{{b}^{2}}-2a{{b}^{3}}-{{b}^{4}}\]
Divide: \[\mathbf{2}{{\mathbf{x}}^{\mathbf{2}}}+\mathbf{3x}+\mathbf{1}\text{ }\mathbf{by}\text{ }\left( \mathbf{x}+\mathbf{1} \right)?\]
(a) \[3x+2\] (b) \[2x+1\]
(c) \[5x-3\] (d) All of these
(e) None of these
Answer (b)
Explanation:
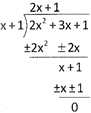
Quotient of the division\[=2x+1\]is the solution of the expression.
Simplify the following, \[{{\mathbf{x}}^{0}}-\mathbf{xy}-\mathbf{8}{{\mathbf{y}}^{0}}.\]
(a) \[\left( xy+7 \right)\]
(b) \[\left( xy-7 \right)\]
(c) \[-\left( xy+7 \right)\]
(d) All of these
(e) None of these
Answer (c)
Explanation: \[{{x}^{0}}-xy-8{{y}^{0}}=1-xy-8=-xy-7=-\left( xy+7 \right).\]
Express the ratio 45 :108 in its simplest form:
(a) 4 : 12 (b) 5 : 12
(c) 5 : 13 (d) 3 : 12
(e) None of these
Answer: (b)
Explanation: In order to express the given ratio in its simplest form we divide its first and second terms by their HCF.
We have, \[45=3\times 3\times 5\] and \[108=2\times 2\times 3\times 3\times 3\]
So, HCF of 45 and 108 is \[3\times 3=9.\]
\[\therefore 45:108=\frac{45}{108}=\frac{45\div 9}{108\div 9}=\frac{5}{12}=5:12\]
Divide Rs. 1250 between Raman and Rahul in the ratio 2 : 3.
(a) Rs. 750 (b) Rs. 745
(c) Rs. 760 (d) Rs. 755
(e) None of these
Answer (a)
Explanation: We have, sum of the terms of the ratio \[=\left( 2+3 \right)=5\]
\[\therefore \] Raman's share \[=Rs.\left( \frac{2}{5}\times 1250 \right)=Rs.\left( 2\times 250 \right)=Rs.500\]
Rahul’s share \[=Rs.\left( \frac{3}{5}\times 1250 \right)=Rs.\left( 3\times 250 \right)=Rs.750\]
You need to login to perform this action.
You will be redirected in
3 sec
