Cubes and Dices
Category : 7th Class
Cubes and Dices
Concept of Cubes
A cube is a three-dimensional figure which has 8 corners, 6 surfaces and 12 edges.
Type I
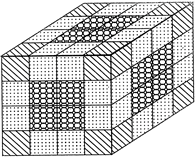
If a cube is painted on all of its surfaces with a colour and then divided into smaller cubes of equal size, then after separation, number of smaller cubes so obtained will be calculated as under:
No. of smaller cubes with three surfaces painted = 8
No. of smaller cubes with one surface painted \[= \left( n - 2 \right)~12\]
No. of smaller cubes with no surface painted \[={{\left( n - 2 \right)}^{2}}~6\]
No. of smaller cubes with no surface painted \[= {{\left( n - 2 \right)}^{3}}\]
Where, n = No. of divisions on the surface of the bigger cube
\[=\frac{length\,of\,edge\,of\,big\,cube}{length\,of\,edge\,of\,one\,smaller\,cube}\]

Type II
If a cube is painted on all of its surfaces with different colours and then divided into various smaller cubes of equal size.
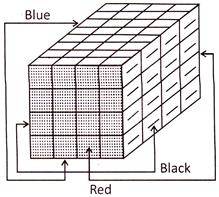
(a) No. of cubes with two surfaces painted with black and blue colours = 8.
(b) No. of cubes with two surfaces painted with blue and red colours = 8.
(c) No. of cubes with two surfaces painted with black and red colours = 8.
And out of this-
(a) No. of cubes with one surface painted with black colour = 8.
(b) No. of cubes with one surface painted with blue colour = 8.
(c) No. of cubes with one surface painted with red colour = 8.
Type III
If a cube is painted on its surfaces in such a way that one pair of opposite surfaces is left unpainted.
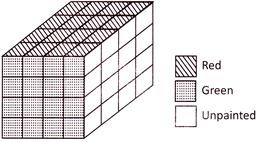
\[=8+\left( n-2 \right)\times ~4=8+8=16\]
\[= \left( n - 2 \right)\times 8 + {{\left( n - 2 \right)}^{2}}\times ~4=2~8 + 4~\times 4 = 16 + 16 = 32.\]
\[= {{\left( n - 2 \right)}^{2}}~\times 2 + {{\left( n - 2 \right)}^{3}}~~~~~~~~~~~~= 4~\times 2 + {{\left( 2 \right)}^{3}}= 8 + 8 = 16.\]
Type IV
If a cube is painted on its surfaces in such a way that one pair of adjacent surfaces is left unpainted.
\[=4+\left( n-2 \right)~\times 5=4+2~\times 5=4+10=14.\]
\[= 4~\times 4 + 2~\times 6 + 2 = 16 + 12 + 2 = 30.\]
\[= {{\left( n - 2 \right)}^{3}}+ {{\left( n - 2 \right)}^{2}}~\times 2 + \left( n - 2 \right) = {{\left( 2 \right)}^{3}}+ {{\left( 2 \right)}^{2}}~\times 2 + 2 = 8 + 8 + 2 = 18.\]
Example
A cube is coloured red on two opposite faces, blue on two adjacent faces and yellow on two remaining faces. It is then cut into cut into two halves along the plane parallel to the red faces. One piece is then cut into four equal cubes and the other one into 32 equal cubes.
Answer the following questions on the basis of given information.
(a) 0 (b) 16
(c) 4 (d) 8
(e) None of these
Ans. (c)
Explanation: (c) Only four smaller cubes from inside the cube will have none of their faces painted.
How many cubes do not have any red faces?
(a) 8 (b) 16
(c) 20 (d) 24
(e) None of these
Ans. (b)
Explanation: (b) 16 cubes from the second layer from the bottom will not have any red face.
How many cubes have at least two coloured faces?
(a) 20 (b) 24
(c) 28 (d) 32
(e) None of these
Ans. (b)
Explanation: (b) No. of at least two coloured faces cubes = No. of three faces coloured cubes + No. of two faces coloured cubes = 8 + 12 = 20.
How many cubes have each a yellow face with other faces without colour?
(a) 4 (b) 12
(c) 16 (d) 18
(e) None of these
Ans. (a)
Explanation: (a) Two cubes each from two yellow faces will have one face painted yellow with other faces without colour. Hence, \[2~\times 2 = 4\] such cubes will be obtained.
How many cubes have at least one face painted blue?
(a) 4 (b) 14
(c) 17 (d) 20
(e) None of these
Ans. (c)
Explanation: (c) Seventeen cubes including four bigger cubes have at least one face painted blue.
Commonly Asked Question
A cube painted red on two adjacent faces and black on the faces opposite to the red faces and green on the remaining faces is cut into 64 smaller cubes of equal size.
Answer the following questions on the basis of given information.
How many cubes are there which have no faces painted?
(a) 0 (b) 4
(c) 8 (d) 16
(e) None of these
Ans. (c)
Explanation: (c) There are 8 cubes with no face painted.
How many cubes have only one face painted?
(a) 8 (b) 16
(c) 24 (d) 32
(e) None of these
Ans. (c)
Explanation: (c) There are 24 cubes having only one face painted.
How many cubes have less than 3 faces painted?
(a) 8 (b) 24
(c) 28 (d) 48
(e) None of these
Ans. (d)
Explanation: (d) There are 24 cubes having only one face painted and 24 cubes having only two faces painted. So the number of cubes having less than 3 faces painted = 24 + 24 = 48.
How many cubes are there with three faces painted?
(a) 4 (b) 8
(c) 16 (d) 24
(e) None of these
Ans. (b)
Explanation: (b) There are 8 cubes having three faces painted.
How many cubes have one face green and one of the adjacent faces black or red?
(a) 8 (b) 16
(c) 24 (d) 28
(e) None of these
Ans. (c)
Explanation: (c) There are 8 + 4 + 4 + 8 = 24 such cubes which have one face green and one of the adjacent faces black or red,
Concept of Dices
A dice is a small throwable object used for generating a random number. It has six faces which show different number of dots from 1 to 6. When thrown or rolled, the die comes to rest showing on its upper surface a random integer from one to six, each value being equally likely. Generally four types of questions can be asked on dices. Let’s study them one by one.
Type 1
In such type of questions, different positions of a dice are shown and we have to identify the position of a number on the dice based on those positions.
Example
If number 2 is marked on the bottom, which number will be on the top?
(i)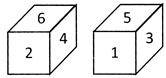 (ii)
(ii)
(a) 1 (b) 3
(c) 4 (d) 5
(e) None of these
Ans. (d)
Explanation: If the figure (i) is rotated in the position of figure (ii) we get number 5 opposite to number 2. If 2 is on the bottom 5 will be on the top.
Commonly Asked Question
On the basis of two figures of dice, you have to tell what number will be on the opposite face of number 5?
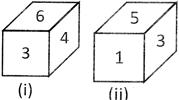
(a) 1 (b) 3
(c) 4 (d) 5
(e) None of these
Ans. (c)
Explanation: Place the common number i.e., 3 to both the dice on the central position of the figure.
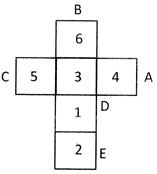
Now place the numbers in the anti-clockwise direction in block A, B and C, D respectively i.e., number 4, 6 being the 1st and 2nd numbers in the anti-clockwise direction of 3 will come in A and B block and like-wise numbers 5 and 1 will come in C and D blocks. And left over number i.e., 2 will come in the block E. Hence, number 4 is opposites to number 5.
Type 2
In such type of questions we have to find the position of a number of the basis of four different position of a dice.
Which number is on the opposite surface of number 3?
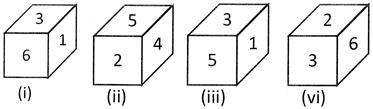
(a) 2 (b) 3
(c) 4 (d) 6
(e) None of these
Ans. (c)
Explanation: Figure (i), (iii) and (iv) show that numbers 6, 1, 5, 2 appear on the adjacent surfaces to the number 3. Hence, 4 will be opposite to number 3.
Which number is opposite to number 5?
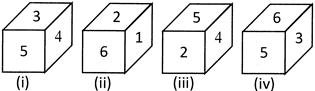
(a) 6 (b) 5
(c) 1 (d) 3
(e) None of these
Ans. (c)
Explanation: From figure (i), (iii) and (iv), it is clear that numbers adjacent to 5 are 3, 4, 2 and 6. Hence, number 1 will be opposite to number 5.
Type 3
In this type of questions, an unfolded dice is given and we have to identify the dice identical to the unfolded dice from the given options.
Example
A figure given below is an unfolded position of a Cubical dice
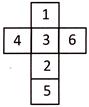
Which of the given dices is identical to the given unfolded dice?
(a) 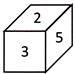 (b)
(b) 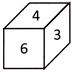
(c) 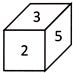 (d)
(d) 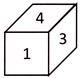
(e) None of these
Ans. (d)
Explanation: From the question figure, it is clear that 4 is opposite to 6, 1 is opposite to 2 and 3 is opposite to 5. Figure (a), (b), (c) will not be identical of question figure because numbers forming the opposite pairs appear on the adjacent surfaces. Hence, figure (d) shows the correct position of the figure unfolded dice shown in question figure.
Commonly Asked Questions
A figure given below is an unfolded position of a cubical dice.
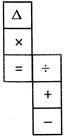
Which one of the following dices is identical to the given unfolded dice?
(a) 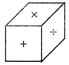 (b)
(b) 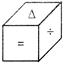
(c) 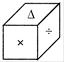 (d)
(d) 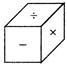
(e) None of these
Ans. (c)
Explanation: A is opposite to =,\[\times \] will be opposite to + and will be opposite to (-). Hence, figure (a), (b), (d) are not identical to question figure, only figure (c) represents the correct position of question figure.
Type 4
In this kind of questions, we have to identify the missing number on a face of dice based on a face of dice based on the two different positions of a dice.
Example
Three positions of the same dice are given below. Observe the figures carefully and tell which number will come in place of (?)?
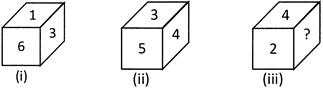
(a) 1 (b) 6
(c) 3 (d) 5
(e) None of these
Ans. (a)
Explanation: From the figure, we see that number 4 has numbers 5, 3, 1 and 2 on the adjacent surfaces and number 6 opposite to it. Comparing the position of dice no. (iii) with this figure, we observe that number 1 will replace (?).
Which letter will come ne the blank surface in figure (iii)?
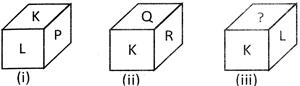
(a) M (b) K
(c) P (d) Q
(e) None of these
Ans. (c)
Explanation: From the figure, we observe that letters L and P are adjacent to the letter K and comparing the figure (iii) of the dice with this figures we see that letter P will replace (?).
You need to login to perform this action.
You will be redirected in
3 sec
