Time Clock and Calendar
Category : 7th Class
Time, Clock and Calendar
Learning Objectives
Time, Clock and Calendar
The face or dial of a watch is a circle whose circumference is divided into 60 equal parts minute spaces.
A clock has two hands, the smaller one is called the hour hand or short hand while the larger one is called the minute hand or long hand.
On the other hand, if it indicates 7.45, when the correct time is 8, it is said to be 15 minutes too slow.
Example
A clock shows the time as 3:30 pm if the minute hand gains 2 minutes every hour, how many minutes will the clock gain by 6 am?
(a) 20 minutes (b) 29 minutes
(c) 30 minutes (d) 35 minutes
(e) None of these
Ans. (b)
Explanation: Hours between 3:30 pm and 6 am are = \[14\frac{1}{2}\]
So, numbers of minutes gained will be = \[14\frac{1}{2}\times 2=29\] minutes.
Two watches, one of which gained at the rate of 1 minute and other lost at the rate of 1 minute daily, were set correctly at noon on the 1st January 1978. When did the watches indicate the same time?
(a) Dec 30, 1978 noon (b) Dec 25, 1978 noon
(c) Dec 27, 1978 noon (d) Dec 26, 1978 noon
(e) None of these
Ans. (c)
Explanation: The first watch gains on the second watch 1 + 1 = 2 minutes in a day.
The watch will indicate the same time when the one has gained 12 hours on the other
As 2 minutes is gained in one day.
So 12 hours is gained \[= 1 / 2\times 12~60 = 360 days\]
Counting 360 days from 1st Jan 1978, we get Dec 27, 1978.
Commonly Asked Questions
How many times do the hands of a clock coincide between 11 O’clock and 1 O’clock?
(a) 0 (b) 1
(c) 2 (d) 3
(e) None of these
Ans. (b)
Explanation: Between 11 O’clock and 1 O’clock the hands of a clock coincide only once. So, the correct answer is (b)
A clock is set right at 5 am. The clock loses 16 minutes in 24 hours. What will be the right time when the clock indicates 10 pm on the 3rd day?
(a) 11:15 pm (b) 11 pm
(c) 12 pm (d) 12:30 pm
(e) None of these
Ans. (b)
Explanation: Time from 5 am of a particular day to 10 pm on the 4th day is 89 hours. Now, the clock loses 16 minutes in 24 hrs or in other words we can say that 23 hours 44 minutes of this clock is equal to 24 hours of the correct clock
Or \[\left( 23\,+\,\,\frac{44}{60}\,\,=\,\,\frac{356}{15} \right)\] hours of this clock = 24 hours of the correct clock
\[\Rightarrow \]89 hours of this clock = \[\left( \frac{24\times 15}{356}\,\times \,\,89 \right)\]hours of correct clock
= 90 hours of the correct clock.
Therefore, it is clear that in 89 hours this clock loses 1 hour and hence the correct time is 11 pm when this clock shows 10 pm.
At what time between 4 and 5 O’clock will the hands of a watch point in opposite directions?
(a) 45 minutes past 4
(b) 40 minutes past 4
(c) \[50\frac{4}{11}\] minutes past 4
(d) \[50\frac{6}{11}\] minutes past 4
(e) None of these
Ans. (d)
Explanation: At 4 O’clock both the hands are 20 minute spaces apart and for having in the opposite-direction they have to be 30 minute spaces apart
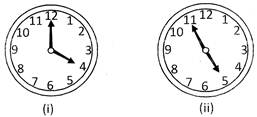
From figure (i) and figure (ii) it is clear/ that minute hand has to travel (20 + 30) minute spaces in order to be in opposite direction to each other. Now 55 minute spaces is gained in 60 minutes.
Therefore, 50 minute spaces will be gained in \[\left( \frac{60}{55}\times 50 \right)\] minutes or \[54\frac{6}{11}\] minutes.
Hence, the hands of the clock will be in opposite direction at \[54\frac{6}{11}\] minutes past 4,
Therefore, (d) is the correct answer.
Find the exact time between 7 am and 8 am when the two hands of a watch meet.
(a) 7 hrs 30.18 minute (b) 7 hrs 35.18 minute
(c) 7 hrs 38.18 minute (d) 7 hrs 25.18 minute
(e) None of these
Ans. (c)
Explanation: At 7 am, the minute hand is 35 minute spaces behind the hour hand 55 minute spaces are gained in 60 minute
So 35 minute spaces will be gained in 38.18 minute.
Calendar
Days in a Week
There are seven days in a week - Sunday, Monday, Tuesday, Wednesday, Thursday, Friday and Saturday.
If today is Monday then,
Example
If the day before yesterday was Thursday, when will Sunday be?
(a) Tomorrow (b) Today
(c) Day after tomorrow (d) Two days after today
(e) None of these
Ans. (a)
Explanation: If day before yesterday was Thursday, then today is Saturday. Therefore, tomorrow will be Sunday.
Suganya went to see a movie nine days age. She goes to the movie only on Thursday. What day of the week is today?
(a) Tuesday (b) Thursday
(c) Friday (d) Saturday
(e) None of these
Ans. (d)
Explanation: Clearly, nine days ago, it was Thursday. Therefore today is Saturday.
Commonly Asked Questions
Today is Wednesday, What will be the day after 98 days?
(a) Sunday (b) Monday
(c) Wednesday (d) Friday
(e) None of these
Ans. (c)
Explanation: Every day of the week is repeated after 7 days. Hence it will be Wednesday, after 98 days.
If 1st October is Sunday, then 1st November will be:
(a) Sunday (b) Monday
(c) Wednesday (d) Friday
(e) None of these
Ans. (c)
Clearly, 1st, 8th, 15th, 22nd and 29th of October are Sundays. So, 31st October is Tuesday. Therefore, 1st November will be Wednesday.
You need to login to perform this action.
You will be redirected in
3 sec
