9th Class Mathematics Related to Competitive Exam Concept of Angles in Trigonometry

       Concept of Angles in Trigonometry

 

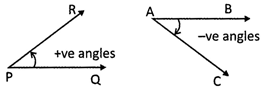
In case of trigonometry, angles may be positive or negative and of any magnitude.  

 

 

            Positive Angles

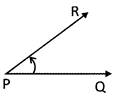
When we measure an angle in anti-clock wise direction it is always positive.

 

 

            Negative Angles

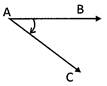
If an angle measures in anti-clock wise direction then it is said to be negative angle.

 

 

            Different Units of Measurement of an Angle

There are three system for measurement of an angle.

1. British System (Sexagesimal System)

2. French System (Centesimal System)

3. Circular Measure or Radian System  

 

British System

It is also known as sexagesimal system. In this system a right angle is divided into 90 equal parts is called degrees.                

\[\text{1}\,\,\text{right}\,\text{angle = 90 }\!\!{}^\circ\!\!\text{ }\]

\[\text{1}{}^\circ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{ = 60 }\!\!'\!\!\text{ }\]

\[\text{1 }\!\!'\!\!\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{ = 60''}\] 

In the above, degree is divided into 60 equal parts known as minutes, and each minute is divided into 60 equal parts known as seconds.  

 

Centesimal System

In this system a right angle is divided into 100 equal parts and each part is known as grade.

\[\text{1}\,\,\text{right}\,\text{angle = 100g}\]

\[\text{1}\,\text{g }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{= 100 }\!\!'\!\!\text{ }\]

\[\text{1}\,'\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{= 100''}\]

 

Radian System

1 radian is defined as an angle which subtend at the centre of a circle by an arc whose length is equal to the length of radius.

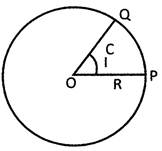
\[\text{PQ = R}\]

We know that \[\text{ }\!\!\pi\!\!\text{ }\] is the ratio of circumference and diameter.

\[\frac{\text{C}}{\text{D}}\,\,\text{=}\,\text{ }\!\!\pi\!\!\text{ }\]

Relation between radian and degree, \[\pi \]radian\[={{180}^{o}}\]

It is also written as

\[{{\text{ }\!\!\pi\!\!\text{ }}^{\text{C}}}\,\text{=}\,\text{180 }\!\!{}^\circ\!\!\text{ }\]

 

Relation between Angle, Length of an Arc and Radius of Circle

We know that the angle formed at the centre is proportional to the length of arc which subtend it.

Means \[\theta \,\,\,\,\alpha \,\,\,\,\,\,l\]

(Here,\[\theta \]represents angle and\[l\]represents the length of arc)

 

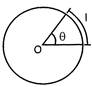
By the definition of radian.

Angle subtended by an arc of length r at the centre of circle = 1 radian.

\[\therefore \] Angle subtended by an arc of length 1 at the centre of circle \[=\frac{1}{\pi }\] radian.

\[\therefore \] Angle subtended by an arc of length (. at the centre of circle \[=\frac{\ell }{r}\]

\[\therefore \] \[\mathbf{\theta  = }\frac{\mathbf{I}}{\mathbf{r}}\]

 

Relation among Different Units of Measurement of an Angle

1. \[{{1}^{o}}=\frac{\pi }{180}\]radian

2. 1 radian \[={{\left( \frac{180}{\pi } \right)}^{0}}\]

3. \[{{\left( \frac{10}{\pi } \right)}^{g}}={{\left( \frac{\pi }{{{180}^{o}}} \right)}^{c}}=1\] degree

It is convention that angles are always measured either in radian or in degree.

 

Conversion of Some Common Angle in Degree into Radian  

Degree	\[{{0}^{o}}\]	\[{{30}^{o}}\]	\[{{45}^{o}}\]	\[{{60}^{o}}\]	\[{{90}^{o}}\]	\[{{180}^{o}}\]	\[{{360}^{o}}\]
Radian	0	\[\frac{\pi }{6}\]	\[\frac{\pi }{4}\]	\[\frac{\pi }{3}\]	\[\frac{\pi }{2}\]	\[\pi \]	\[2\pi \]

 

 

 

In the ancient times different geometrical structures were made. In these structures one of the most famous is the Great pyramid of Giza. It is the oldest and larges pyramid in the Giza. This was built as a tomb for fourth dynasty Egyptian king khafu and constructed over a 20 year period concluding around 2560 BC. The great pyramid was the tallest man-made structure in the world for over 3,800 years.  

 

 

• When we measure an angle in anti-clock wise direction it is always positive.
• If an angle measures in anti-clock wise direction then it is said to be negative angle.
• \[{{1}^{o}}=\frac{\pi }{180}radian\]
• \[1\,radian=\left( \frac{{{180}^{o}}}{\pi } \right)\]
• \[\theta =\frac{\ell }{r}\]  

 

 

  Find the ratio of radii of two circles, if arc of equal length subtend angles \[\text{3}0{}^\circ \] and \[\text{45}{}^\circ \] at their centre.

(a) 2:3                                                  

(b) 4:3         

(c) 3:2                                                   

(d) 3 :4

(e) None of these  

 

Answer: (c)  

Explanation:

Suppose radii of circles be \[{{r}_{1}}\]and\[{{r}_{2}}\]

then \[{{\theta }_{1}}=\frac{l}{{{r}_{1}}}\]and\[{{\theta }_{2}}=\frac{l}{{{r}_{2}}}\]

where \[{{\theta }_{1}}={{30}^{o}},{{\theta }_{2}}={{45}^{o}}\]

\[\frac{{{\theta }_{1}}}{{{\theta }_{2}}}=\frac{\frac{l}{{{r}_{1}}}}{\frac{l}{{{r}_{2}}}}\]

\[\Rightarrow \] \[\frac{{{\theta }_{1}}}{{{\theta }_{2}}}=\frac{{{r}_{2}}}{{{r}_{1}}}\]        \[\Rightarrow \] \[\frac{{{r}_{1}}}{{{r}_{2}}}=\frac{{{\theta }_{2}}}{{{\theta }_{1}}}\]          \[\Rightarrow \]\[\frac{{{r}_{1}}}{{{r}_{2}}}=\frac{{{\bcancel{45}}^{{{3}_{o}}}}}{{{\bcancel{30}}_{2}}^{o}}\]

\[\Rightarrow \] \[\frac{{{r}_{1}}}{{{r}_{2}}}=\frac{3}{2}\]

\[{{r}_{1}}:{{r}_{2}}=3:2\]  

 

 

  The measures of two angles of a triangle are \[\text{6}0{}^\circ \text{ 53}'\text{ 51}''\] and \[\text{51}{}^\circ \text{ 22}'\text{ 5}0''\] respectively. The measure of third angle in radian is____.

(a) 1.15 radian                                  

(b) 11 radian

(c) 180 radian                                    

(d) 11.5 radian

(e) None of these  

 

Answer: (a)  

Explanation: 

The sum of two angles \[=[(\text{62}''\text{ 53}'\text{ 51}'')+\text{51}{}^\circ \] \[\text{22}'\text{ 5}0'']=\text{114}{}^\circ \text{ 16}'\text{ 41}''\]  

Third angle of triangle \[=\text{18}0{}^\circ -(\text{14}0{}^\circ \text{ 16}'\text{ 41}'')\]) \[=\text{65}{}^\circ \text{ 43}'\text{ 19}''\]

\[={{\left( 65+\frac{43}{60}+\frac{19}{3600} \right)}^{0}}=\frac{234000+2580+19}{3600}=\]\[{{\left( \frac{236599}{3600} \right)}^{0}}={{(65.722)}^{0}}\]  

We know that

\[{{1}^{o}}=\frac{\pi }{180}\]radian

\[\text{(65}.\text{722}){}^\circ =\left( \frac{\pi }{180}\times 65.722 \right)\]radian = 1.15 radian (approx)    

 

 

  lf the ratio of radii of two circles are in 5 : 4 then the angle subtend at the centre of circles by the same arc length be _____.

(a) \[\text{75}{}^\circ ,\text{ 6}0{}^\circ \]                                           

(b) \[\text{45}{}^\circ ,\text{ 6}0{}^\circ \]       

(c) \[\text{6}0{}^\circ ,\text{ 45}{}^\circ \]                                          

(d) \[\text{6}0{}^\circ ,\text{ 75}{}^\circ \]

(e) None of these  

 

Answer: (d)  

 

 

  The distance travelled by the tip of minute hand in 10 minutes when the length of it is 20 cm, is _____.

(a) 20.95m                                          

(b) 20.95cm     

(c) 2.095cm                                        

(d) 209.5cm

(e) None of these  

 

Answer: (b)  

 

 

  The diameter of the wheel of a bicycle is 40 cm. The speed of bicycle if it makes \[\frac{1}{2}\] revolution in 10 second is ______.

(a) \[4\pi \frac{cm}{\min }\]                                       

(b) \[0.4\pi \frac{cm}{\sec }\]

(c) \[4\pi \frac{m}{\operatorname{s}}\]                                               

(d) \[4\pi \frac{cm}{\sec }\]

(e) None of these  

 

Answer: (d)