Solids
Category : 9th Class
Solids
The objects having definite shape and size are called solids. A solid occupies a definite space.
Cuboid
Solids like matchbox, chalk box, a tile, a book an almirah, a room etc. are in the
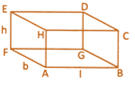
Shape of a cuboid
Formulae
For cuboid of length = I, breath = b and height = h, we have:
(i) Volume \[=(l\times b\times h)\]
(ii) Total surface area \[=2(lb\times bh\times lh)\]
(iii) Lateral surface area \[=[2(l+b)\times h]\]
Cube
Solids like ice cubes, sugar cubes, dice etc. are the shape of cube Formula for a cube having each edge = a units, we have:
(i) Volume\[={{a}^{3}}\]
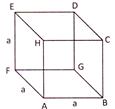
(ii) Total surface area \[=6{{a}^{2}}\]
(iii) Lateral surface area \[=4{{a}^{2}}\]
Cylinder
Solids like measuring jar, circular pencils, circular pipes, road rollers, gas cylinder, are said to have a cylindrical shape. Formula for a cylinder of base radius = r & height (or length) = h, we have
(i) Volume\[=\pi {{r}^{2}}h\]
(ii) Curved surface area \[=2\pi rh\]
(iii) Total surface area \[=(2\pi rh+2\pi {{r}^{2}})=2\pi r(h+r)\]
Hollow Cylinder
Solids like a hollow cylinder having external radius = R, internal radius = r & height = h then , we have
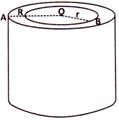
(i) Volume of material = (external volume) - (internal volume) \[=(\pi {{R}^{2}}h-\pi {{r}^{2}}h)=\pi h({{R}^{2}}-{{r}^{2}})\]
(ii) Curved surface area of hollow cylinder = (external surface area) - (internal surface area) \[=(2\pi Rh-2\pi rh)=2\pi h(R-r)\]
(iii) Total surface area of hollow cylinder = (curved surface area) + 2\[\times \](area of the base ring) \[=2\pi h(R-r)+2(\pi {{R}^{2}}-\pi {{r}^{2}})\] \[=2\pi (R-r)(R+r+h)\]
Cone
Consider a cone in which base radius = r, height = h & slant height\[l=\sqrt{{{h}^{2}}+{{r}^{2}}}\] then we have
(i) Volume of the cone \[=\frac{1}{3}\pi {{r}^{2}}h\]
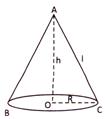
(ii) Curved surface area of the cone \[=\pi rl\]
(iii) Total surface area of the cone = (curved surface area) + (area of the base) \[\pi rl+\pi {{r}^{2}}=\] \[\pi r(l+r)\]
Sphere
Objects like a football, a cricket ball, etc. are said to have the shape of the a sphere. For a sphere of radius r, we have
(i) Volume of the sphere \[=\left( \frac{4}{3}\pi {{r}^{3}} \right)\]
(ii) Surface area of the sphere \[(4\pi {{r}^{2}})\]
Hemisphere
A plane through the centre of a sphere cuts it into two equal parts, each part is called hemisphere. For a hemisphere of radius r, we have:
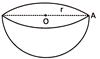
(i) Volume of the hemisphere \[=\frac{2}{3}\pi {{r}^{3}}\]
(ii) Curved surface area of the hemisphere \[=(2\pi {{r}^{2}})\]
(iii) Total surface area of the hemisphere \[=(3\pi {{r}^{2}})\]
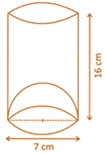
The inner diameter of a glass is 7 cm and it has a raised portion at the bottom in the shape of a hemisphere as shown in the figure. If the height of the glass is 16 cm then find the apparent capacity and the actual capacity of the glass.
(a) \[\text{616 c}{{\text{m}}^{\text{3}}},\text{ 526}.\text{17 c}{{\text{m}}^{\text{3}}}\]
(b) \[~\text{616 c}{{\text{m}}^{\text{3}}},\text{ 1527}.\text{95 c}{{\text{m}}^{\text{3}}}\]
(c) \[\text{616 c}{{\text{m}}^{\text{3}}},\text{ 886}.\text{16 c}{{\text{m}}^{\text{3}}}\]
(d) \[\text{616 c}{{\text{m}}^{\text{3}}},\text{ 9}.\text{58 c}{{\text{m}}^{\text{3}}}\]
(e) None of these
Answer: (a)
Explanation:
In the given figure
radius of the glass\[=\frac{7}{2}\]cm & height = 16 cm
Apparent capacity of the glass\[=\pi {{r}^{2}}h\]
\[\text{=}\left( \frac{22}{7}\times \frac{7}{2}\times \frac{7}{2}\times \text{l6} \right)\text{c}{{\text{m}}^{\text{3}}}\text{=616 c}{{\text{m}}^{\text{3}}}\]
Volume of the hemisphere at the bottom
\[\text{=}\frac{2}{3}\pi {{r}^{3}}\left( \frac{2}{3}\times \frac{22}{7}\times \frac{7}{2}\times \frac{7}{2} \right)\text{c}{{\text{m}}^{\text{3}}}\text{=}\frac{539}{6}\text{c}{{\text{m}}^{\text{3}}}=89.83\,c{{m}^{3}}\]
A actual capacity of the glass = (volume of the glass) - (volume of the hemisphere) = (616 - \[\text{89}.\text{83})\text{c}{{\text{m}}^{\text{3}}}\text{ 526}.\text{17c}{{\text{m}}^{\text{3}}}\]
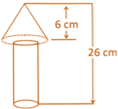
A wooden toy is in the shape of a cone surmounted on a cylinder as shown in figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that on the cylinder part of radius 4 cm. Find the surface area of the toy.
(a) \[\text{264}\,\text{c}{{\text{m}}^{\text{2}}}\]
(b) \[\text{25}0\,\text{c}{{\text{m}}^{\text{2}}}\]
(c) \[\text{322}.\text{14}\,\text{c}{{\text{m}}^{\text{2}}}\]
(d) \[\text{25}0\,\text{c}{{\text{m}}^{\text{2}}}\]
(e) None of these
Answer: (c)
Explanation:
Area of conical part of toy = (upper area of cone) + (base area of the cone) - (base area of cylinder\[=(\pi Rl+\pi {{R}^{2}}-\pi {{r}^{2}})\]sq units When
R = Radius of the conical part = 2.5 cm
H = Height of the conical part = 6 cm
L= Slant height of the conical part\[=\sqrt{{{R}^{2}}+{{h}^{2}}}\]\[=\sqrt{{{(2.5)}^{2}}+{{6}^{2}}}\]=6.5 cm
R = Radius or cylinder = 2 cm
Area\[=\pi (Rl+{{R}^{2}}-{{r}^{2}})\]
\[=\frac{22}{7}\left\{ 2.5\times 6.5+{{(2.5)}^{2}}-{{2}^{2}} \right\}c{{m}^{2}}=\frac{407}{7}c{{m}^{2}}\]\[=\text{58}.\text{14 c}{{\text{m}}^{\text{2}}}\]
Area of cylindrical part = (curved surface area of the cylinder) + (area of the base of the cylinder) \[=2\pi rh+\pi {{r}^{2}}\]
When h = height of cylinder = (26 - 6) = 20 cm
\[=\pi r(2h+r)\text{c}{{\text{m}}^{\text{2}}}=\left\{ \frac{22}{7}\times 2\times (40+2) \right\}c{{m}^{2}}=\text{264}\,\text{c}{{\text{m}}^{\text{2}}}\]
Then total surface area = Area of upper part + Area of lower part
\[=\text{58}.\text{14 }{{\text{m}}^{\text{2}}}+\text{264 }{{\text{m}}^{\text{2}}}=\text{322}.\text{14 c}{{\text{m}}^{\text{2}}}\]
The base of a triangular field is twice its altitude. If the cost of ploughing the field at Rs. 3.75 per 100 \[{{m}^{2}}\] is Rs 13500. Find the altitude and the base of the field
(a) 1240m, 400m
(b) 1200 m, 600 m
(c) 1350m, 200m
(d) 9050 m, 100 m
(e) None of these
Answer: (b)
Explanation:
The cost of ploughing is Rs 3.75, if area=100\[{{\text{m}}^{\text{2}}}\]
If the cost of ploughing is Rs 1, area\[=\left( \frac{100}{3.75} \right){{m}^{2}}\]
If the cost of ploughing is Rs 13500, area\[=\left( \frac{100}{3.75}\times 13500 \right){{m}^{2}}=360000\,{{m}^{2}}\]
area of the field\[=\text{36}0000\text{ }{{\text{m}}^{\text{2}}}\]
Let the Altitude of the field be\[x\]meters
Then base\[=2x\]meters
Area of the field\[=\left( \frac{1}{2}\times 2x\times x \right){{m}^{2}}=({{x}^{2}}){{m}^{2}}\]
\[{{x}^{2}}=360000\] \[\Rightarrow \]\[x=\sqrt{360000}=600\]
altitude = 600 m, base = 1200 m
Each side of an equilateral triangle measures 10 cm. Calculate
(i) The area of triangle &
(ii) The height of the triangle
Given: \[\sqrt{3}=1.732\]
(a) 18.65cm
(b) 18.85cm
(c) 8.99cm
(d) 18.66cm
(e) None of these
Answer: (b)
Explanation
Here, a = 10 cm
(i) Area of the triangle\[=\left( \frac{\sqrt{3}}{4}\times {{a}^{2}} \right)\]
\[=\left( \frac{\sqrt{3}}{4}\times 10\times 10 \right)c{{m}^{2}}=(25\times \sqrt{3})c{{m}^{2}}\]
\[=(25\times 1.732)c{{m}^{2}}=43.3c{{m}^{2}}\]
(ii) Height of the triangle\[=\left( \frac{\sqrt{3}}{2}\times a \right)\]units
\[=\left( \frac{\sqrt{3}}{2}\times 10 \right)cm=(5\times \sqrt{3})cm=(5\times 1.732)cm=8.66\,cm\]
The height of an equilateral triangle is 6 cm. Find the area of the triangle, correct to two decimal places take \[\sqrt{3}=\text{1}.\text{732}\]
(a) \[\text{2}0.\text{88}\,\text{c}{{\text{m}}^{\text{2}}}\]
(b) \[\text{2}0.\text{78}\,\text{c}{{\text{m}}^{\text{2}}}\]
(c) \[\text{2}0.\text{78}\,\text{c}{{\text{m}}^{\text{2}}}\]
(d) \[\text{2}0.\text{78}\,\text{c}{{\text{m}}^{\text{4}}}\]
(e) None of these
Answer: (b)
Find the area of an isosceles triangle, each of whose equal sides is 3 cm and base is 24 cm.
(a) 3.42
(b) 3.50
(c) 3.62
(c) 3.30
(d) None of these
Answer: (d)
The minute hand of a clock \[\frac{x}{2}\]cm long. Find the area of the face of the clock described by the minute hand in 35 minutes
(a) \[\frac{11{{x}^{2}}}{24}\]
(b) \[\frac{7{{x}^{2}}}{24}\]
(c) \[\frac{5{{x}^{2}}}{24}\]
(d) \[\frac{13{{x}^{2}}}{24}\]
(e) None of these
Answer: (a)
You need to login to perform this action.
You will be redirected in
3 sec
