Trigonometrical Identities
Category : 10th Class
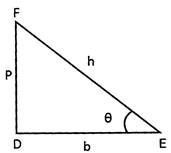
In the adjoining figure triangle DEF is a right angled triangle right angle at D. Then the trigonometrical identities are
1. \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
2. \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
3. \[co{{\sec }^{2}}\theta -{{\cot }^{2}}\theta =1\]
We can also derive different relations between identities in different form
(a) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
or \[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \]
or \[\sin \theta =\pm \sqrt{1-{{\cos }^{2}}\theta }\]
Similarly
\[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]
or \[\cos \theta =\pm \sqrt{1-{{\sin }^{2}}\theta }\]
(b) \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
or \[{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \]
or \[{{\sec }^{2}}\theta =\sqrt{1+{{\tan }^{2}}\theta }\]
Similarly
\[{{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1\]
or \[\tan \theta =\pm \sqrt{{{\sec }^{2}}\theta -1}\]
(c) \[\cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]
or \[\cos e{{c}^{2}}\theta =1+{{\cot }^{2}}\theta \]
or \[\cos e{{c}^{2}}\theta =\pm \sqrt{1+{{\cot }^{2}}\theta }\]
Similarly
\[{{\cot }^{2}}\theta =\cos e{{c}^{2}}\theta -1\]
or \[\cot \theta =\pm \sqrt{\cos e{{c}^{2}}\theta -1}\]
Verification of \[\mathbf{si}{{\mathbf{n}}^{\mathbf{2}}}\mathbf{\theta +co}{{\mathbf{s}}^{\mathbf{2}}}\mathbf{\theta =1}\]
Suppose \[\Delta \text{RST}\] is a right angled triangle in which right angle at R and angle S in formed at\[\theta \].
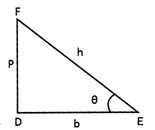
Here, perpendicular RT represented by "p", base RS represented by "b" and hypotenuse "ST" represented by h.
Then by Pythagoras theorem,
\[{{p}^{2}}+{{b}^{2}}={{h}^{2}}\]
As we know
\[\sin \theta =\frac{p}{h},\] \[\cos \theta =\frac{b}{h}\]
Therefore,
\[{{\sin }^{2}}\theta =\frac{{{p}^{2}}}{{{h}^{2}}}\,\,\text{and}\,\,{{\cos }^{2}}\theta =\frac{{{b}^{2}}}{{{h}^{2}}}\]
\[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =\frac{{{p}^{2}}}{{{h}^{2}}}+\frac{{{b}^{2}}}{{{h}^{2}}}=\frac{{{p}^{2}}+{{b}^{2}}}{{{h}^{2}}}=\frac{{{h}^{2}}}{{{h}^{2}}}=1\]
Therefore, \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
Similarly we can verify other results.
![]() Values of Different Trigonometrical Ratios in Different Quadrants
Values of Different Trigonometrical Ratios in Different Quadrants
Above shows the different quadrants. The following are about the T- Ratios when angles lies in different quadrants
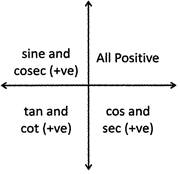
1. When the angle lies in the I quadrant all trigonometrical ratios are positive i.e. The value of \[\text{sin}\theta ,\text{ cos}\theta ,\text{ tan}\theta ,\text{ cot}\theta ,\text{ sec}\theta \]and \[\text{cosec}\theta \] are positive.
2. When the angle\[''\theta ''\] lies in the second quadrant, the value of sine and cosec are positive and other ratios like \[\text{cos}\theta ,\text{ tan}\theta ,\text{ cot}\theta \] and \[\text{sec}\theta \] are negative.
3. When an angle \[''\theta ''\] lies in third quadrant, the value of tan e and cote are positive and other ratios like \[\text{sin}\theta \text{,}\,\text{cos}\theta ,\text{ cosec}\theta \]and \[\sec \theta \] are negative.
4. When an angle \[''\theta ''\] lies in fourth quadrant, the value of \[\text{cos}\theta \text{ sec}\theta \] are positive and other ratios like \[\text{sin}\theta ,\text{ tan}\theta ,\text{ cosec}\theta \] and cote are negative.
From the figure given below you can remember it easily
You need to login to perform this action.
You will be redirected in
3 sec
