Distance -Time Graph for Uniform Motion
Category : 9th Class
Distance - Time Graph for Uniform Motion
A public transport bus is traveling from terminus P to terminus Q. The following observation was recorded by a passenger in the bus..
Observations
| Distance in km | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| Time | 10.00 am | 10.10 am | 10.20 am | 10.30 am | 10.40 am | 10.50 am | 11.00 am |
From the above table it is clear that the bus is covering equal distances in equal intervals of time i.e., the bus is moving with uniform speed. If the bus continues to move with uniform speed, we can calculate the distance covered by the bus at any time.
Let us consider an object moving with uniform speed v from its initial position \[{{S}_{1}}\] to final positions \[{{S}_{2}}\] in time \[{{t}_{1}}\] and \[{{t}_{2}}\].
then, uniform speed \[=\,\frac{\text{Total Distance}}{\text{Total Time}}\]
\[V=\frac{{{S}_{2}}-{{S}_{1}}}{{{t}_{2}}-{{t}_{1}}}\]
\[{{S}_{2}}-{{S}_{1}}=V\,({{t}_{2}}-{{t}_{1}})\] …………………….(1)
The equation (1) gives the relation between distance, time and average speed. Let us now plot a distance-time graph for the above illustration. A distance time graph is a line graph showing the variation of distance with time. In a distance-time graph, time is taken along x-axis and distance along y-axis.
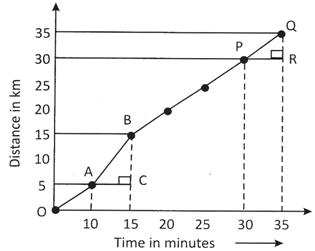
The slope of the graph \[=\frac{BC}{AC}=\frac{s}{t}=\,\text{speed}\]
Calculation
Consider another two A and B on the graph and construct a right – angled triangle ABC.
Speed \[=\frac{40-30}{10}=\frac{10}{10}\,=\,\text{1}\,\text{km/min}\]
Consider another two points P and Q on the graph and construct a right angled triangle PRQ.
Slope = Speed \[=\frac{QR}{PR}=\frac{35-30}{60-50}=\frac{15}{10}=1.5\,\,\text{km/min}\]
This shows that speed is not uniform.
Now, let us consider the nature of S-t graph for non-uniform motion.
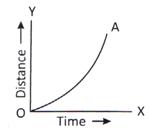
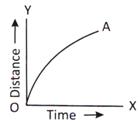
Figure (a) Figure (b)
From figure (a), the S-t graph represents the speed of a moving object increases with time.
From figure (b), the S-t graph represents the speed of a moving object decreases with time.
From the nature of S-t graph we can conclude whether the object is moving with uniform speed or non uniform speed.
The figure given below represents the different route a student can choose from his home to the school.
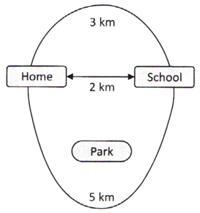
Martin goes to school on his bike with an average speed of 45 km/h. By using the relation. \[\text{Speed}\,\,\text{= }\,\frac{\text{Distance}}{\text{Time}}\] one, can find out the time required to reach the school. But if you are not sure of the route which one would have been taken/ then it is not possible.
Thus, by just giving the speed of a moving object it is not possible to locate the exact position of the object at a given time. So, there arises a need to define a quantity. which has both magnitude as well as direction. The physical quantity which has both magnitude and direction is called vector quantity Thus Velocity is defined as the distance covered by a moving object in a particular direction in unit time or speed in a particular direction.
\[\text{Velocity}\,\,\text{=}\,\,\frac{\text{Displacement}}{\text{Time}}\]
In a body travels a distance ‘s’ in a given direction in time t, then its velocity ‘v’ is given by :
\[V=\frac{s}{t}\]
Where, V = velocity of the body, it is a vector quantity.
S = displacement
and t = time taken (to travel that distance;
SI unit of velocity is m/s (meter/second).
\[[\because \] SI unit of distance is meter and that of time is second]
Thus we can say that the difference between speed and velocity is that speed has only magnitude but no direction, whereas velocity has magnitude as well as direction.
Average Velocity
It is defined as the ratio of the total displacement of the body to the total time taken by the body, to travel the distance.
Average Velocity = \[\frac{\text{Total Placement}}{\text{Total Time}}\]
Or, Average Velocity \[\frac{\text{Initial velocity }+\text{ final velocity}}{2}\]
Or, \[{{V}_{av}}=\frac{u+v}{2}\]
Where, u = initial velocity and v = final velocity
Uniform Velocity
A body is said to have uniform velocity if it travels equal distance in equal interval of time, no matter how small is the time interval.
The velocity of a body can be changed in two ways:
Non-Uniform Velocity
A body is said to be moving with non uniform velocity if it covers unequal distance in equal time interval.
Difference between Speed and Velocity
| S. No. | Speed | S. No. | Velocity |
| 1. | Distance traveled by an object per unit time is known as its speed. | 1. | The distance traveled by an object in a particular direction (i.e. displacement) per unit time is known as its velocity. |
| 2. | Average speed of a moving object cannot be zero. | 2. | Average velocity of a moving object can be zero. |
| 3. | Speed tells how fast an object moves. | 3. | Velocity tells how fast an object moves and in which direction it moves; |
| 4. | Speed is a scalar quantity. | 4. | Velocity is a vector quantity. |
| 5. | Speed of an object is always positive | 5. | Velocity of an object can be positive and negative. |
Thus, we can conclude that Speed and Velocity are not always equal in magnitude.
The magnitude of speed and velocity of a moving body is equal only if the body moves in a single straight line. If however, a body does not move in a single straight line, then the speed and velocity of the body are not equal.
A bus travels a distance of 250000 meter from Mumbai to Nagpur in 300 minutes. Find the speed and velocity of the bus for the entire journey.
(a) 50km/h and50km/h due North
(b) 25 km/h and 50 km/h due South
(c) 50 km/h and-50 km/h due west
(d) 250 km/h and 250 km/h due North
(e) None of these
Answer: (a)
Explanation
(i) \[Speed\,=\frac{Dis\tan ce}{Time}\,=\frac{250\,km}{5h}=50\,km/h\]
Thus, the speed (or average speed) of the car is 50 km/h.
(ii) Velocity \[=\frac{\text{Displacement}}{\text{Time}}\]
\[=\frac{\text{25}0\text{ km towards North}}{\text{5}\,\text{h}}\]
= 50 km/h towards North
So, the velocity (or average velocity) of the car is 50 km/h towards North.
A bus moving towards its destination travels first 40 km at the uniform speed of 55 km/h and nest 20 km at the uniform speed of 50 km/h. Find the total time taken by the bus to reach its destination.
(a) 1.2 hours
(b) 1.34 hours
(c) 1.127 hours
(d) 1.565 hours
(e) None of these
Answer: (c)
Explanation
For uniform speed, \[S=V\times t\]
Time taken to travel first 40 km \[=\frac{40}{55}=\frac{8}{11}\] hours
Time taken to travel next 20 km \[=\frac{20}{50}=\frac{2}{5}\] hours
The total time taken is \[=\frac{2}{5}+\frac{8}{11}=\frac{62}{55}\] hours = 1.127 hours
You need to login to perform this action.
You will be redirected in
3 sec
