JEE Main & Advanced Physics Ray Optics Photometry

The branch of optics that deals with the study and measurement of the light energy is called photometry.

(1) Radiant flux (R) : The total energy radiated by a source per second is called radiant flux. It's S.I. unit is Watt (W).

(2) Luminous flux \[(\phi )\] : The total light energy emitted by a source per second is called luminous flux. It represents the total brightness producing capacity of the source. It's S.I. unit is Lumen (lm).

(3) Luminous efficiency \[(\eta )\] : The Ratio of luminous flux and radiant flux is called luminous efficiency i.e. \[\eta =\frac{\varphi }{R}\].

Luminous flux and efficiency

(4) Luminous Intensity (L) : In a given direction it is defined as luminous flux per unit solid angle i.e.

\[L=\frac{\varphi }{\omega }\to \frac{\text{Light energy}}{\sec \,\times \text{solid angle }}\xrightarrow{\text{S}\text{.I}\text{. unit}}\frac{\text{lumen}}{\text{steradian}}=\text{candela}\,\text{(}Cd\text{)}\]

The luminous intensity of a point source is given by : \[L=\frac{\varphi }{4\pi }\]\[\Rightarrow \]\[\varphi =4\pi \times (L)\]

(5) Illuminance or intensity of illumination (I) : The luminous flux incident per unit area of a surface is called illuminance.  \[I=\frac{\varphi }{A}\]. It's S.I. unit is \[\frac{\text{Lumen}}{{{m}^{\text{2}}}}\] or Lux (ix) and it's C.G.S. unit is Phot.   \[1\,\text{Phot}={{10}^{4}}\text{Lux}=\frac{\text{1}\,\text{Lumen}}{c{{m}^{\text{2}}}}\]

(i) Intensity of illumination at a distance r from a point source is  \[I=\frac{\varphi }{4\pi {{r}^{2}}}\Rightarrow I\propto \frac{1}{{{r}^{2}}}\].

(ii) Intensity of illumination at a distance r from a line source is \[I=\frac{\varphi }{2\pi rl}\Rightarrow I\propto \frac{1}{r}\]

(iii) In case of a parallel beam of light \[I\propto {{r}^{0}}\].

(iv) The illuminance represents the luminous flux incident on unit area of the surface, while luminance represents the luminous flux reflected from a unit area of the surface.

(6) Relation Between Luminous Intensity (L) and Illuminance (I) : If S is a unidirectional point source of light of luminous intensity L and there is a surface at a distance r from source, on which light is falling normally.

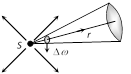
(i) Illuminance of surface is given by : \[I=\frac{L}{{{r}^{2}}}\]

(ii) For a given source L = constant so \[I\propto \frac{1}{{{r}^{2}}}\] ; This is called. Inverse square law of illuminance.

(7)  Lambert/s Cosine Law of Illuminance : In the above discussion if surface is so oriented that light from the source falls, on it obliquely and the central ray of light makes an angle \[\theta \] with the normal to the surface, then                

(i) Illuminance of the surface \[I=\frac{L\cos \theta }{{{r}^{2}}}\]

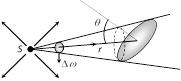
(ii) For a given light source and point of illumination (i.e. L and r = constant) \[I\propto \cos \theta \] this is called Lambert's cosine law of illuminance. \[\Rightarrow {{I}_{\max }}=\frac{L}{{{r}^{2}}}={{I}_{o}}(\text{at}\theta \,={{\text{0}}^{\text{o}}})\]

(iii) For a given source and plane of illuminance (i.e. L and h = constant)

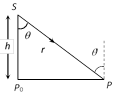
\[\cos \theta =\frac{h}{r}\] so \[I=\frac{L}{{{h}^{2}}}{{\cos }^{3}}\theta \]

or \[I=\frac{Lh}{{{r}^{3}}}\] i.e. \[I\propto {{\cos }^{3}}\theta \] or \[I\propto \frac{1}{{{r}^{3}}}\]  

(8) Photometer and Principle of Photometry : A photometer is a device used to compare the illuminance of two sources.

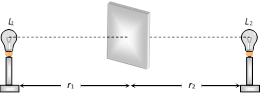
Two sources of luminous intensity \[{{L}_{1}}\], and \[{{L}_{2}}\]are placed at distances \[{{r}_{1}}\] and \[{{r}_{2}}\] from the screen so that their flux are perpendicular to the screen. The distance \[{{r}_{1}}\] and \[{{r}_{2}}\] are adjusted till \[{{I}_{1}}={{I}_{2}}\]. So \[\frac{{{L}_{1}}}{r_{1}^{2}}=\frac{{{L}_{2}}}{r_{2}^{2}}\Rightarrow \]\[\frac{{{L}_{1}}}{{{L}_{2}}}={{\left( \frac{{{r}_{1}}}{{{r}_{2}}} \right)}^{2}}\] ; This is called principle of photometry.