Measurements and Motion
Category : UPSC
MEASUREMENTS AND MOTION
MEASUREMENTS
The process of comparing an unknown physical quantity with respect to a known quantity is known as measurement. When we say that the length of our bedroom is 10 feet it implies that the bedroom is 10 times the known quantity ?foot? (feet is the plural of foot). So, measurement of any physical quantity consists of two parts - (i) a numerical value and (ii) the known quantity. The known quantity is called the unit of that physical quantity. Measurement is an integral part of physics.
Physics is the foundation on which engineering, technology and other sciences are based.
PHYSICAL QUANTITIES
Quantities which can be measured are called physical quantities. Velocity, acceleration, force, area, volume, pressure, etc. are some examples of physical quantities.
Kinds of Physical Quantities
There are two kinds of physical quantities
Fundamental physical quantities: Fundamental physical quantities are those which do not depend on other quantities and also independent of each other. They are seven in number viz; length, mass, time, thermodynamic temperature, electric current, luminous intensity and amount of substance.
Derived physical quantities: Derived physical quantities are those which are derived from fundamental physical quantities. For example, velocity is derived from the fundamental quantities length and time, hence it is a derived physical quantity.
UNITS
To measure a physical quantity it is compared with a standard quantity. This standard quantity is called the unit of that quantity. For example, to measure the length of a desk, it is compared with the standard quantity known as ?metre?. Thus, ?metre? is said to be the unit of length.
Types of Units
There are two types of units:
Fundamental units: Fundamental units are those units which cannot be derived from any other unit, and they cannot be resolved into any basic or fundamental unit. Also, the units of fundamental physical quantities are called fundamental units.
The following table shows the seven fundamental units of S.I. System
|
S. No. |
Fundamental Physical quantity |
Fundamental Unit |
Symbol |
|
1. |
Length |
meter |
m |
|
2. |
Mass |
kilogram |
kg |
|
3. |
Time |
second |
s |
|
4. |
Electric current |
ampere |
A |
|
5. |
Temperature |
kelvin |
K |
|
6. |
Luminous intensity |
candela |
cd |
|
7. |
Amount of substance |
mole |
mol |
Derived units: Any unit which can be obtained by the combination of one or more fundamental units are called derived unit.
Examples: Area, speed, density, volume, momentum, acceleration, force etc.
Derived units of some physical quantities are as follows:
|
S. No. |
Derived Physical quantity |
Derived Unit |
|
1. |
Area |
\[{{m}^{2}}\] |
|
2. |
Volume |
\[{{m}^{3}}\] |
|
3. |
Density |
Kg /\[{{m}^{3}}\] |
|
4. |
Speed |
m/s |
|
5. |
Acceleration |
m/\[{{s}^{2}}\] |
|
6. |
Momentum |
Kg m/ s |
|
7. |
Force |
kg m/\[{{s}^{2}}\] or newton |
|
8. |
Work |
kg \[{{m}^{2}}/{{s}^{2}}\] or joule |
|
9. |
Power |
kg \[{{m}^{2}}/{{s}^{3}}\]or watt |
|
10. |
Charge |
ampere-sec or coulomb |
|
11. |
Potential |
joule/coulomb or volt |
|
12. |
Resistance |
volt/ampere or ohm |
Systems of Units
Depending upon the units of fundamental physical quantities, there are four main systems of units, namely
The first three of these systems recognize only three fundamental quantities i.e. length (L), mass (M) and time (T) while the last one recognizes seven fundamental quantities, i.e. length (L), mass (M), time (T), electric current (I or A) thermodynamic temperature (K or\[\theta \]), amount of substance (mol) and luminous intensity (\[{{I}_{v}}\]). An international organization, the Conference Generate des Poids et Mesures, or CGPM is internationally recognized as the authority on the definition of units. In English, this body is known as “General Conference on Weights and Measure”. The System International de Unites, or SI system of units, was set up in 1960 by the
CGPM.
Characteristics of a Standard Unit
A standard unit must have following features to be accepted world wide. It should
Supplementary Units of SI System
The following table shows the two supplementary units of SI. System.
|
S. No. |
Physical quantity |
Supplementary Unit |
Symbol |
|
1. |
Plane angle |
radian |
rad |
|
2. |
Solid angle |
steradian |
sr |
Practical Units of Length
Astronomical unit, AU: The average distance between the sun and the earth about \[1.49\times {{10}^{11}}\]m is called 1 AU.
Parsec: The parsec is defined to be the distance at which a star would have a parallax angle equal to one second of arc.
1 Parsec = \[3.08568025\times {{10}^{16}}\] m.
Light year: The light year is the distance travelled by light in one year. All electromagnetic waves travel at a speed of 299,792,458 \[m{{s}^{-1}}\]and an average year being 365.25 days.
One light year is \[299,792,458\times {{10}^{8}}m{{s}^{-1}}\times (365.25\times 24\times 60\times 60)s=9.46073\times {{10}^{15}}m\]or \[9.46073\times {{10}^{12}}km\].
Angstrom: An angstrom is a unit of length used to measure small lengths such as the wavelengths of light, atoms and molecules.
One angstrom,\[\text{1}\overset{\text{o}}{\mathop{\text{A}}}\,={{10}^{-10}}m\].
Fermi: A unit of length used to measure nuclear distance = \[{{10}^{-15}}\]meter, 1 fermi = \[{{10}^{-15}}\]m.
PREFIXES FOR SI UNITS
In Physics we have to deal from very small (micro) to very large (macro) magnitudes. To express such large and small magnitudes simultaneously we use following prefixes:
When a prefix is placed before the symbol of unit, the combined prefix and symbol should be considered as one new symbol which can be raised to a positive or negative power without any bracket, e.g., \[k{{m}^{3}}\]mean \[{{({{10}^{3}}m)}^{3}}\]but never \[{{10}^{3}}{{m}^{3}}\].
ERRORS IN MEASUREMENTS
Generally measured value of a quantity is different from the true value of the physical quantity. The difference between the true value and measured value is called error. Error = true value - measured value
Before we discuss about errors let us understand two important terms:
Accuracy: It is the measure of how close the measured value is to the true value of the physical quantity.
Precision: It tells us about the limit or resolution up to which the quantity is measured.
Significant Figures
Significant digits or figures give information about the accuracy of a measurement. It tells us about the number of digits in which we have confidence. Suppose a particular measurement is reported to be 9.28 cm, then the two digits 9 and 2 are reliable and certain while the digit 8 is uncertain. The reliable and first uncertain digits are known as significant digits or figures.
There are certain rules for counting significant digits or figure:
Rule-1. All the non-zero digits are significant—For example 2134 has four significant figures and 27184 has five significant figures.
Rule-2. All the zeros between two non-zero digits are significant, no matter where the decimal point is, if at all. For example 25089 has five significant figures, 12.0021 has six significant figures.
Rule-3. In a number which is less than one all zeros to the right of decimal point but to the left of a non-zero digit are not significant.
Rule-4. All the zeros on the right of last non-zero digits are significant in a number with a decimal point. For example in 3.500 there are four significant digits and in 0.079000 there are five significant figures.
Rule-5. All the zeros on the right on a non-zero digit are not significant in a number without decimal point. For example 15800 has only three significant figures, 18930000 has only four significant figures.
Rule-6. All the zeros on the right on a non-zero digit are taken to be significant when these come from a measurement. For example some distance is measured to be 7890 m then this number would have four significant figures.
Rule-7. A change of system of units does not change the number of significant digits in a measurement. Also when a number is written in scientific notation (\[a\times {{10}^{b}}\]) then the powers of 10 are irrelevant to the determination of significant figures.
Least Count (L.C.)
The smallest division on the scale of the measuring instrument. It is an uncertainty associated with the resolution of the measuring instrument.
DIMENSIONS OF A PHYSICAL QUANTITY
All physical quantities can be expressed in terms of the fundamental quantities. Consider the physical quantity force.
\[Force=mass\times acceleration=mass\times \frac{velocity}{time}\]
\[=mass\times \frac{length/time}{time}=mass\times length\times tim{{e}^{-2}}\]
\[\therefore =Unit\,of\,force=unit\,of\,mass\times unit\,of\,length\times {{(unit\,of\,time)}^{-2}}\]
Thus we can express the unit of force as products of different power of the fundamental units of mass, length and time. i.e., Force = \[[ML{{T}^{-2}}]\]
Thus the dimensions of a physical quantity are the powers to which the fundamental quantities mass, length and time must be raised to represent it.
Science in Action
A spring balance on the moon will give different reading from that on Earth but a beam balance will give the same reading as spring balance requires gravity to measure. Mass remains same throughout but weight changes with gravity. Mass will only change if there is any change in the volume of matter in the body.
MOTION
REST AND MOTION
Rest: An object is said to be at rest if it does not change its position with respect to its surroundings with the passage of time.
Motion: A body is said to be in motion if its position changes continuously with respect to the surroundings (or with respect to an observer) with the passage of time.
Rest and motion are relative terms.
Types of Motion on the basis of Dimensions
One-Dimensional Motion: It is the motion in which the position of the object changes only in one direction. In this case the object moves along a line. For example- motion of a tram along a straight line, freely falling object under gravity, etc.
Two-Dimensional Motion: It is the motion in which the position of the object changes in two directions. In this case the object moves on a plane. For example - projectile motion.
Three-Dimensional Motion: It is the motion in which the position of the object changes in three directions. In this case the object moves in a space. For example - a bird flying in the sky.
DISTANCE AND DISPLACEMENT
Motion is related to change of position. The length travelled in changing position may be expressed in terms of distance, i.e., the actual path length between two points.
Distance is a scalar quantity, which has only a magnitude with no direction.
The direct straight line pointing from the initial point to the final point is called displacement (change in position). Displacement only measures the change in position, not the details involved in the change in position.
Displacement is a vector quantity, which has both magnitude and direction.
The displacement can be zero, even if the distance is not zero. For example when a body is thrown vertically upwards from a point on the ground, after sometime it returns back to the same point, then the displacement of the body is zero but the distance travelled by the body is not zero, it is 2h if h is the maximum height attained by the body.
Similarly, if a body is moving in a circular or closed path and reaches its original position after one revolution, then the displacement in one revolution is zero, but the distance travelled is equal to the circumference of the circular path =\[2\pi r\]if r is the radius of the circular path.
Handy Facts
The actual distance travelled by an object in a given time interval can be equal to or greater than the magnitude of displacement. It can never be less than the magnitude of displacement.
The displacement of an object in a given tome interval can be positive, zero or negative. However, distance covered by the object in a given time interval is always positive.
UNIFORM AND NON-UNIFORM MOTION
Uniform Motion
It is a motion in which a body moves in a straight line (rectilinear) and covers equal distances in equal intervals of time.
The path length of a body in a uniform rectilinear motion is equal to the magnitude of the displacement. Consequently, the path length(s) in the motion is equal to the magnitude of the velocity (v) multiplied by the time (t) i.e., s = vt.
Handy Facts
No force is required to keep an object in uniform motion. When an object has uniform motion along a straight line in a given direction, the magnitude of displacement is equal to actual distance covered.
Non-Uniform Motion
If a body covers unequal distances in equal intervals of time, it is said to be moving with a non-uniform motion. It is a motion in which the velocity varies with time. The change in the velocity of a body in non-uniform motion is characterized by acceleration. Uniformly variable motion is a motion with a constant acceleration. Uniformly variable motion can be curvilinear like circular motion. If a uniformly variable motion is rectilinear, i.e., the velocity v changes only in magnitude, it is convenient to take the straight line in which a material point moves as one of the coordinate axes (say, the x-axis).
THE RATE OF MOTION
Average Speed
It is defined as the total distance travelled divided by the time interval to travel that distance.
Average speed\[{{V}_{av}}=\frac{d}{t},d\]is distance travelled, and t is time interval (change in time).
The average speed of Cheetah is 70 m/s for 30 seconds
Instantaneous Speed
It is the speed at a particular time instant (t is infinitesimal small or close to zero).
Uniform and Non-uniform Speed
A body is said to be moving with uniform speed if it covers equal distances in equal time intervals and with non-uniform or variable speed if covers unequal distances in the same time intervals.
SPEED WITH DIRECTION (VELOCITY)
Average Velocity
It is defined as the ratio of change in position or displacement to the time taken.
\[\bar{v}={{v}_{av}}=\frac{{{x}_{2}}-{{x}_{1}}}{{{t}_{2}}-{{t}_{1}}}=\frac{\Delta x}{\Delta t}\]
Here \[{{x}_{1}}\] and \[{{x}_{2}}\]are the positions of the particle at time \[{{t}_{1}}\]and\[{{t}_{2}}\]respectively. Also, \[\Delta x={{x}_{2}}-{{x}_{1}}\]= change in position and\[\Delta t={{t}_{2}}-{{t}_{1}}\]= change in time. Its unit is\[m{{s}^{-1}}\],\[cm{{s}^{-1}}\] or\[km\,{{h}^{-1}}\].
Instantaneous Velocity
Velocity of a body at a particular instant or moment of time is called instantaneous velocity.
RATE OF CHANGE OF VELOCITY
[ACCELERATION]
Positive acceleration: If the velocity of an object increases in the same direction, the object has a positive acceleration.
Negative acceleration (Retardation): If the velocity of a body decreases in the same direction, the body has a negative acceleration or it is said to be retarding e.g., a train slows down.
GRAPHICAL REPRESENTATION OF MOTION IN A STRAIGHT LINE
Displacement-Time Graphs
A graph showing the displacement of the cyclist from A to C: This graph shows us how, in t second time, the cyclist has moved from A to C.
We know the gradient (slope) of a graph is defined as the change in y divided by the change in x,
i.e., \[\frac{\Delta y}{\Delta x}\]

In this graph the gradient of the graph is just\[\frac{\Delta \vec{s}}{\Delta t}\] and this is just the expression for velocity.
The slope of a displacement-time graph gives the velocity.
The slope is the same all the way from A to C, so the cyclist?s velocity is constant over the entire displacement he travels.
Observe the following displacement-time graphs.
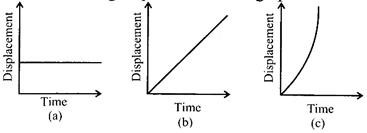
Graph (a) shows the object is stationary over a period of time. The gradient is zero, so the object has zero velocity.
Graph (b) shows the object is moving at a constant velocity. You can see that the displacement is increasing as time goes on. The gradient, however, stays constant so the velocity is constant. Here the gradient is positive, so the object is moving in the direction we have defined as positive.
Graph (c) shows the object is moving at a constant acceleration. You can see that both the displacement and the velocity (gradient of the graph) increases with time.
The gradient is increasing with time, thus the
Handy Facts
The x-t graph of an object having uniform motion is a straight line inclined to the time-axis. The slope of straight line x-t graph gives velocity of the uniform motion of the object.
Velocity Velocity-Time Graphs
This is the velocity-time graph of a cyclist travelling from A to B at a constant acceleration, i.e. with steadily increasing velocity.
The gradient of this graph is just \[\frac{\Delta \vec{s}}{\Delta t}\]and this is just the expression for acceleration. Because the slope is the same at all points on this graph, the acceleration of the cyclist is constant.
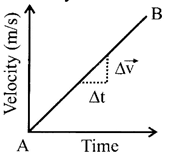
The slope of a velocity-time graph gives the acceleration. Observe the following velocity-time graphs.
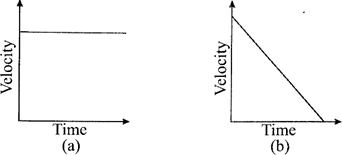
Graph (a) shows the object is moving at a constant Velocity over a period of time. The gradient is zero, so the object is not accelerating.
Graph (b) shows an object which is decelerating. You can see that the velocity is decreasing with time. The gradient, however, stays constant so the acceleration is constant. Here the gradient is negative, so the object is accelerating in the opposite direction to its motion, hence it is decelerating.
Acceleration-Time Graphs
Observe the following acceleration-time graphs.
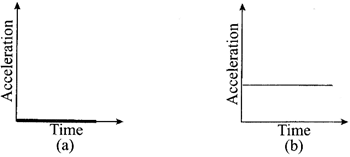
Graph (a) shows an object which is either stationary or travelling at a constant velocity. Either way, the acceleration is zero over time.
Graph (b) shows an object moving at a constant acceleration. In this case the acceleration is positive – remember that it can also be negative.
EQUATIONS OF MOTION
Kinematic equations can be used to describe the motion with constant acceleration.
First equation (Equation for velocity-time relation): Final velocity
= initial velocity + acceleration x time interval or v = u + at
Second equation (Equation for position-time relation):
Displacement = initial velocity x time interval +\[\frac{1}{2}\]\[\times \]acceleration \[\times \] \[time\text{ }interva{{l}^{2}}\] or \[s=ut+\frac{1}{2}a{{t}^{2}}\]
Third equation (Equation for position-velocity relation): \[{{v}^{2}}={{u}^{2}}+2as\]
\[Final\text{ }velocit{{y}^{2}}\text{ }=\text{ }initial\text{ }velocit{{y}^{2}}\text{ }+\]
\[2\text{ }\times \text{ }acceleration\text{ }\times \text{ }displacement\]
Or \[{{v}^{2}}={{u}^{2}}+2as\]
RELATIVE MOTION
The motion of an object B w.r.t. object A which is moving or stationary is called as relative motion.
Relative velocity of an object B w.r.t. object A when both are in motion is the rate of change of position of object B w.r.t. object A. Relative velocity of object B w.r.t. object A, \[\overrightarrow{{{V}_{BA}}}=\overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{A}}}\]
MOTION UNDER GRAVITY
It is a common experience that when a body is dropped form a certain height it experiences acceleration due to gravity and its motion is in a straight path. Similarly, when a body is thrown vertically up, it goes to a certain height and then starts falling again, experiencing acceleration due to gravity throughout the motion.
The value of acceleration due to gravity (g) is taken as 9.8\[m/{{s}^{2}}\], 980 \[cm/{{s}^{2}}\]or 32\[ft/{{s}^{2}}\].
Let us consider the three cases discussed below.
Case-1: Body thrown downward: In this case, initial motion of the body is downward so according to the sign convention, downward direction will be taken as positive and upward direction as negative. So, the kinematic equations will be:
(i) \[v=u+gt\]
(ii) \[h=ut+\frac{1}{2}g{{t}^{2}}\]
(iii) \[{{v}^{2}}={{u}^{2}}+2gh\]
(iv) \[{{h}^{nth}}=h+\frac{1}{2}g(2n-1)\]
In a special case when the body is dropped/let falls i.e., initial velocity (u) = 0, then equation becomes
\[v=gt;h=\frac{1}{2}g{{t}^{2}};{{v}^{2}}=2gh;{{h}^{nth}}=\frac{1}{2}g(2n-1)\]

Science in Action
According to Galileo, when two bodies of different masses are dropped from the same height both will touch the floor at the same time in the absence of air resistance. If a ping pong and basketball are dropped the floor from same height, they will hit at the same time in the absence of air resistance.
Case-II: Body thrown upward:
If a body is thrown vertically up with an initial velocity (u). Hence a = - g. Kinematic equations will be:
(i) \[v=u-gt\] (ii) \[h=ut-\frac{1}{2}g{{t}^{2}}\]
(iii) \[{{v}^{2}}-{{u}^{2}}=-2gh\] (iv) \[{{h}_{n}}=u-g\left( n-\frac{1}{2} \right)\]
Maximum height reached by the body
From equation \[{{v}^{2}}={{u}^{2}}+2gh\]
\[H=\frac{{{u}^{2}}}{2g}\] \[[\therefore v=0]\]
Therefore, the maximum height reached by the body is directly proportional to the square of the initial velocity.
Time of ascent (\[{{t}_{a}}\]): The time taken by a body thrown up to reach maximum height ‘h’ is called its time of ascent.
\[{{t}_{a}}=\frac{u}{g}\]
Hence time of ascent \[{{t}_{a}}\] is directly proportional to the initial velocity u.
Time of descent (\[{{t}_{d}}\]): The time taken by a freely falling body to reach the ground is called the time of descent.
\[{{t}_{d}}=\sqrt{\frac{2h}{g}}\]
and \[h=\frac{{{v}^{2}}}{2g},{{t}_{d}}=\frac{v}{g}\]
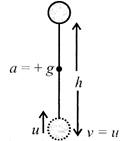
But, we know that u = v i.e., projected velocity of a body is equal to the velocity of the body on reaching the ground.
\[\therefore \] \[{{t}_{d}}=\frac{u}{g}=time\,of\,ascwnt\,({{t}_{a}})\]
Time of ascent = time of descent
Case-III: Body projected vertically up from the top of a tower:
If a body is projected vertically up from the top of a tower of height ‘h’ with velocity ‘u’. Then
Displacement after time t is \[s=ut-\frac{1}{2}g{{t}^{2}}\]
Velocity after time t is \[v=u-gt\].
Velocity on reaching the ground is \[\sqrt{{{u}^{2}}+2gh}\]
Maximum height above the ground is \[\left\{ h+({{u}^{2}}/2g) \right\}\]
PROJECTILE MOTION
Projectile is the name given to a body thrown with some initial velocity in any arbitrary direction and then allowed to move under the influence of a constant acceleration. The motion of a projectile is called projectile motion.
Example: A football kicked by the player, a stone thrown from the top of building, a bomb released from a plane.
The path followed by a projectile is called its trajectory, mostly, the trajectory of a projectile is parabolic.
Maximum height (H): When a projectile moves, it covers a maximum distance in vertical direction. This maximum distance is called the maximum height attained by the projectile.
Maximum height \[H=\frac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}\]
Horizontal range (R): The horizontal distance between the point of projection and the point of landing of a projectile.
Maximum range\[R=\frac{{{u}^{2}}{{\sin }^{2}}2\alpha }{g}\]
Time of flight (T): The time taken by the projectile to reach the point of landing from the point of projection.
Time of flight \[T=\frac{2u\sin \alpha }{g}\]
Science in Action
You need to login to perform this action.
You will be redirected in
3 sec
