-
question_answer1)
From a distance of 100 m from the foot of a building, the angle of elevation of its top is \[\text{3}0{}^\circ \]. What is the height of the building?
A)
\[57.7\,m\] done
clear
B)
\[100\sqrt{3}\,m\] done
clear
C)
\[5.77\,m\] done
clear
D)
\[\frac{100}{3}\,m\] done
clear
View Solution play_arrow
-
question_answer2)
The angles of elevation of the top from two points on either side of a tree are\[\text{3}0{}^\circ \]and\[\text{6}0{}^\circ \]. What is the height of the tree if the two points are 52 m apart?
A)
39 m done
clear
B)
22.5 m done
clear
C)
65 m done
clear
D)
225 m done
clear
View Solution play_arrow
-
question_answer3)
The angle of depression of a car from the top of a 20 m high tower is\[\text{6}0{}^\circ \]. At what distance from the foot of the tower is the car?
A)
16m done
clear
B)
8m done
clear
C)
22m done
clear
D)
12m done
clear
View Solution play_arrow
-
question_answer4)
The height of a kite from the ground is 100 Vim. If the angle of elevation from a point on the ground is\[\text{45}{}^\circ \], what is the length of the string of the kite?
A)
\[100\sqrt{3}\,m\] done
clear
B)
\[100\sqrt{2}\,m\] done
clear
C)
\[100\sqrt{6}\,m\] done
clear
D)
100 m done
clear
View Solution play_arrow
-
question_answer5)
A 24 m tall tree was cut to a height from the ground. The top of the tree touching the ground makes an angle\[\text{3}0{}^\circ \]with the ground. At what height from the ground was the tree cut?
A)
4 m done
clear
B)
8 m done
clear
C)
10 m done
clear
D)
6 m done
clear
View Solution play_arrow
-
question_answer6)
A person standing on the bank of a river observes that the angle of elevation of the top of a tower on the opposite bank is\[\text{3}0{}^\circ \]. He moves 40 m towards the bank and finds the angle of elevation to be\[\text{6}0{}^\circ \]. What is the width of the river?
A)
24 m done
clear
B)
20 m done
clear
C)
26 m done
clear
D)
15 m done
clear
View Solution play_arrow
-
question_answer7)
The angles of elevation of the sun changes from\[\text{45}{}^\circ \]to\[\text{3}0{}^\circ \].Then the shadow of a tower on the ground increases by 10 m. What is the height of the tower?
A)
13.65m done
clear
B)
13.56m done
clear
C)
15.63m done
clear
D)
15.36m done
clear
View Solution play_arrow
-
question_answer8)
From an aero plane at an altitude of 900 m, two cars moving towards it in the same direction are found to be\[\text{6}0{}^\circ \]and\[\text{45}{}^\circ \]. What is the distance between the cars?
A)
415m done
clear
B)
315.4m done
clear
C)
380.4 m done
clear
D)
305 m done
clear
View Solution play_arrow
-
question_answer9)
From a tower of 200 m, the angles of depression of two buildings in opposite sides of the tower are found to be\[\text{6}0{}^\circ \]and\[\text{45}{}^\circ \]. What is the distance between the buildings?
A)
415m done
clear
B)
315.4m done
clear
C)
200 m done
clear
D)
305 m done
clear
View Solution play_arrow
-
question_answer10)
The angles of elevation of the top of a building from the ground floor and first floor of another building are\[\text{6}0{}^\circ \]and\[\text{45}{}^\circ \] respectively. If the first floor is 40 m above the ground floor, what is the height of the building?
A)
54.64m done
clear
B)
94.64m done
clear
C)
40m done
clear
D)
109.3m done
clear
View Solution play_arrow
-
question_answer11)
From two opposite ends of a 100 m wide road, the angles of elevation of the top of a clock tower are found to be\[\text{3}0{}^\circ \]and\[\text{45}{}^\circ \]. What is the height of the clock tower?
A)
36.6 m done
clear
B)
36 m done
clear
C)
37 m done
clear
D)
35.4 m done
clear
View Solution play_arrow
-
question_answer12)
Two buildings are 140 m apart. The angle of elevation of the top of a building as seen from the top of the other is\[\text{3}0{}^\circ \]. If the second building is 60 m tall, how tall is the first building?
A)
83 m done
clear
B)
80.83 done
clear
C)
84m done
clear
D)
140.83 done
clear
View Solution play_arrow
-
question_answer13)
What is the angle of elevation of a light source when the length of the shadow of a flag post is equal to its height?
A)
\[\text{45}{}^\circ \] done
clear
B)
\[\text{3}0{}^\circ \] done
clear
C)
\[\text{6}0{}^\circ \] done
clear
D)
(d)\[\text{9}0{}^\circ \] done
clear
View Solution play_arrow
-
question_answer14)
A ladder 19 m long is placed leaning against a wall. If the angle of elevation of the ladder is\[\text{6}0{}^\circ \], how far is the ladder from the wall?
A)
11 m done
clear
B)
9.5 m done
clear
C)
10.5 m done
clear
D)
9 m done
clear
View Solution play_arrow
-
question_answer15)
A gas balloon is tied with a 215 m long rope with an inclination of\[\text{45}{}^\circ \]with the horizontal. How high is the balloon?
A)
166m done
clear
B)
178m done
clear
C)
152m done
clear
D)
184m done
clear
View Solution play_arrow
-
question_answer16)
From a 50 m tall building, the angles of depression of the top and foot of a temple are found to be 30° and 60° respectively. What is the height of the temple?
A)
36m done
clear
B)
25.3m done
clear
C)
33.33m done
clear
D)
30m done
clear
View Solution play_arrow
-
question_answer17)
The angle of elevation of a flag on a school building is\[~\text{45}{}^\circ \]. Moving 40 m towards the building, the angle of elevation is found to be\[\text{6}0{}^\circ \]. What is the height of the flag from the ground?
A)
40 m done
clear
B)
94.64 m done
clear
C)
60 m done
clear
D)
54.64 m done
clear
View Solution play_arrow
-
question_answer18)
The angle of elevation of the top of a 'Br tower from the foot of a hillock is\[\text{6}0{}^\circ \]. The angle of elevation of the top of the hillock from the foot of the tower is\[\text{3}0{}^\circ \]. If the hillock is 50 m, what is the height of the tower?
A)
50m done
clear
B)
140m done
clear
C)
100m done
clear
D)
150m done
clear
View Solution play_arrow
-
question_answer19)
From a 200 m tall tower, the angles of depression of the top and bottom of a pole are\[\text{3}0{}^\circ \]and\[\text{6}0{}^\circ \]respectively. What are the respective values of height and distance of the pole from the tower?
A)
133.33m, 115.46m done
clear
B)
115.46m, 133.33m done
clear
C)
115.33 m, 66.33m done
clear
D)
145.46m.33m done
clear
View Solution play_arrow
-
question_answer20)
The string of a kite is 200m long. It makes an angle of\[\text{3}0{}^\circ \]with the ground. What is the height of the kite above the ground?
A)
120m done
clear
B)
150m done
clear
C)
100m done
clear
D)
200m done
clear
View Solution play_arrow
-
question_answer21)
An eagle flying at an altitude of 1200 m flies vertically above another eagle at the same time, when the angles of elevation of the two birds are\[\text{6}0{}^\circ \]and\[\text{45}{}^\circ \] respectively. How high above the second eagle is the first eagle flying?
A)
507.20 m done
clear
B)
500 m done
clear
C)
570.81 m done
clear
D)
300 m done
clear
View Solution play_arrow
-
question_answer22)
A 15 m long ladder placed vertically along a wall broke in such a way that its top touches the ground making an angle of\[\text{6}0{}^\circ \]with it. At what height from the ground did the ladder break?
A)
7.34m done
clear
B)
8m done
clear
C)
9.46 m done
clear
D)
6.96 m done
clear
View Solution play_arrow
-
question_answer23)
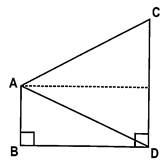
From a window A, 10 m above the ground, the angle of elevation of the top C of a tower is \[\text{x}{}^\circ \], where \[\tan x{}^\circ =\frac{5}{2}\], and the angle of depression of the foot D of the tower is \[\text{y}{}^\circ \], where tan \[\text{tan}\,\text{y}{}^\circ =\frac{1}{4}\]. What is the height CD of the tower to the nearest metre?
A)
135m done
clear
B)
75m done
clear
C)
59m done
clear
D)
110m done
clear
View Solution play_arrow
-
question_answer24)
PQ is a tower standing on a horizontal plane, Q being the foot of the tower. A and B are two points on the plane such that\[\angle \text{BQP}\] is\[\text{9}0{}^\circ \], AB = 4 m. If \[\cot (\angle PAQ)=\frac{3}{10}\]and\[\cot (\angle PBQ)=\frac{1}{2}\], find the height of the tower.
A)
10m done
clear
B)
15m done
clear
C)
18m done
clear
D)
20m done
clear
View Solution play_arrow
-
question_answer25)
The distance between two vertical poles is 60 m. The height of one of the poles is double the height of the other. The angles of elevation of the tops of the poles from the middle point of the line segment joining their feet are complementary to each other. Find the heights of the poles.
A)
21.21 m, 42.42m done
clear
B)
36.63 m, 67.76 m done
clear
C)
42.24m.10.01 m done
clear
D)
16.16m, 22.22m done
clear
View Solution play_arrow
-
question_answer26)
The shadow of a person X, when the angle of elevation of the sun is a, is equal in length to the shadow of person Y, when angle of elevation of the sun is\[\left( \frac{\alpha }{2} \right)\]. Which one of the following is correct?
A)
X is shorter than Y. done
clear
B)
X is twice as tall as Y. done
clear
C)
X is taller than Y but is not twice as tall as Y. done
clear
D)
Both X and Y are of equal of height. done
clear
View Solution play_arrow
-
question_answer27)
Two observers are stationed north of a tower at a distance of 20 m from each other. If the elevation of the tower observed by them are \[\text{3}0{}^\circ \]and\[\text{45}{}^\circ \], respectively, find the height of the tower.
A)
10m done
clear
B)
16.32m done
clear
C)
\[10(\sqrt{3}+1)m\] done
clear
D)
30m done
clear
View Solution play_arrow
-
question_answer28)
If the angle of depression and elevation of the top of a tower of height 'h' from the top and bottom of a second tower are x and y respectively, find the height of the second tower.
A)
\[h(\cot y-\cot x)\] done
clear
B)
\[h(\tan x+\tan y)\] done
clear
C)
\[h(1+\tan x\cot y)\] done
clear
D)
\[h(\tan y.\cot x+1)\] done
clear
View Solution play_arrow
-
question_answer29)
Two posts are 25m and 15m high and the line joining their tops makes an angle of\[\text{45}{}^\circ \]with the horizontal. What is the distance between these posts?
A)
5 m done
clear
B)
\[\frac{10}{\sqrt{2}}m\] done
clear
C)
10m done
clear
D)
\[10\sqrt{2}\,m\] done
clear
View Solution play_arrow
-
question_answer30)
The angle of elevation of the top of an incomplete tower at a point 40 m from its base is\[\text{45}{}^\circ \]. If the elevation of the completed tower at the same point is\[\text{6}0{}^\circ \], find the height through which the tower has been raised.
A)
\[40\sqrt{3}m\] done
clear
B)
\[40(\sqrt{3}+1)m\] done
clear
C)
\[40\left( 1-\frac{1}{\sqrt{3}} \right)m\] done
clear
D)
\[40(\sqrt{3}-1)m\] done
clear
View Solution play_arrow
-
question_answer31)
The angle of elevation of an object from a point 500 m above a lake is observed to be \[\text{3}0{}^\circ \] and the angle of depression of its reflection in the lake is\[~\text{45}{}^\circ \]. Find the height of the object above the lake.
A)
\[\frac{500}{\sqrt{3}}(1+\sqrt{3})m\] done
clear
B)
\[500(2+\sqrt{3})m\] done
clear
C)
\[500(3+\sqrt{3})m\] done
clear
D)
\[500(4+\sqrt{3})m\] done
clear
View Solution play_arrow
-
question_answer32)
A flag - staff is fixed at the top of a tower. The angles of elevation of the top and the bottom of this flag-staff at a point distant 'a' m from the foot of the tower, are\[\alpha \]and\[\beta \], respectively. Find the height of the flag -staff (in m).
A)
\[a(\sin \alpha -\sin \beta )\] done
clear
B)
\[a(\cos \beta -\cos \alpha )\] done
clear
C)
\[a(\tan \alpha -\tan \beta )\] done
clear
D)
\[a\tan (\alpha -\beta )\] done
clear
View Solution play_arrow
-
question_answer33)
The height of a tower is h m and the angle of elevation of the top of the tower is a. On moving a distance h/2 towards the tower, the angle of elevation becomes P. What is the value of\[\cot \alpha -\cot \beta \]?
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{2}{3}\] done
clear
C)
1 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer34)
From the top of a 60 m high tower, the angle of depression of the top and bottom of a building are observed to be\[\text{3}0{}^\circ \]and\[\text{6}0{}^\circ \] respectively. Find the height of the building.
A)
\[60\sqrt{3}\,m\] done
clear
B)
\[40\sqrt{3}\,m\] done
clear
C)
40 m done
clear
D)
20 m done
clear
View Solution play_arrow
-
question_answer35)
A landmark on the bank of a river is observed from two points X and Y on the opposite banks of the river. The lines of sight make equal angles with the bank of the river. If XY = 1 km, what is the width of the river?
A)
\[\frac{3}{2}km\] done
clear
B)
\[\frac{1}{2}km\] done
clear
C)
\[\frac{3\sqrt{2}}{2}km\] done
clear
D)
\[\frac{3\sqrt{3}}{2}km\] done
clear
View Solution play_arrow
-
question_answer36)
A person standing on the bank of a river finds that the angle of elevation of the top of a tower on the opposite bank is\[\text{45}{}^\circ \]. Which of the following is true?
A)
Breadth of the river is twice the height of the tower. done
clear
B)
Height of the river is twice the breadth of the river. done
clear
C)
The height of the tower and the breadth of the river are equal. done
clear
D)
Breadth of river is thrice the height of the tower. done
clear
View Solution play_arrow
-
question_answer37)
The angles of elevation of the top of a vertical tower from points at distance a and b from the base and in the same line with it are complementary. If a > b, find the height of the tower.
A)
\[\sqrt{ab}\] done
clear
B)
\[\sqrt{(a+b)}\] done
clear
C)
\[\sqrt{(a/b)}\] done
clear
D)
\[\sqrt{(b-a)}\] done
clear
View Solution play_arrow
-
question_answer38)
A tower subtends an angle of\[~\text{3}0{}^\circ \]at a point on the same level as the foot of the tower. At a second point h m above the first, the depression of the foot of the tower is 60°. What is the horizontal distance of the tower from the point?
A)
\[\text{h cot 6}0{}^\circ \] done
clear
B)
\[\text{h cot 3}0{}^\circ \] done
clear
C)
\[\frac{h}{2}\text{cot 6}0{}^\circ \] done
clear
D)
\[\frac{h}{2}\text{cot 3}0{}^\circ \] done
clear
View Solution play_arrow
-
question_answer39)
Starting from the same point in a leveled field, Rahul walked 1000 m due East and then 1000 m due North whereas Aryan walked 2000 m North-East. At the end of the walks, what is the distance between Rahul and Aryan?
A)
Zero done
clear
B)
828 m done
clear
C)
586m done
clear
D)
1000m done
clear
View Solution play_arrow
-
question_answer40)
If a flag staff of 6 m height placed on the top of a tower throws a shadow of \[2\sqrt{3}m\]along the ground, find the angle that the sun makes with the ground.
A)
\[\text{6}0{}^\circ \] done
clear
B)
\[\text{3}0{}^\circ \] done
clear
C)
\[\text{45}{}^\circ \] done
clear
D)
\[~\text{9}0{}^\circ \] done
clear
View Solution play_arrow
-
question_answer41)
The angle of elevation of a jetfighter from a point P on the ground is\[\text{6}0{}^\circ \]. After five seconds of flight, the angle of elevation changes to\[\text{45}{}^\circ \]. If the jet is flying at a height of 3000 m. find the speed of the jet, in m/s.
A)
\[1000(3-\sqrt{3})\] done
clear
B)
\[200(3-\sqrt{3})\] done
clear
C)
\[1000\sqrt{3}\] done
clear
D)
\[600\] done
clear
View Solution play_arrow
-
question_answer42)
The angles of elevation of the tops of two pillars of height h and 2h from a point on the line joining the feet of the two pillars are complementary. lf the distances of the feet of the pillars from that point are x and y respectively, find the value of 2h2.
A)
\[{{x}^{2}}y\] done
clear
B)
\[x{{y}^{2}}\] done
clear
C)
\[xy\] done
clear
D)
\[{{x}^{2}}{{y}^{2}}\] done
clear
View Solution play_arrow
-
question_answer43)
A round balloon of radius 'r' subtends an angle\[\alpha \]at the eye of an observer, while the angle of elevation of its centre is\[\beta \]. Find the height of the centre of the balloon.
A)
\[r\sin \frac{\alpha }{2}\cos ec\beta \] done
clear
B)
\[r\cos ec\frac{\alpha }{2}\cos \beta \] done
clear
C)
\[r\cos \frac{\alpha }{2}\cos ec\beta \] done
clear
D)
\[r\cos ec\frac{\alpha }{2}\sin \beta \] done
clear
View Solution play_arrow
