-
question_answer1)
| Directions: Q. 1 to 5 |
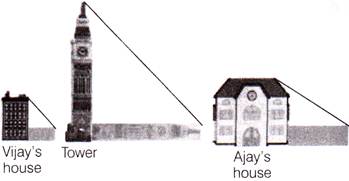
| Vijay is trying to find the average height of a tower near his house. |
| He is using the properties of similar triangles. The height of Vijay's house, if 20 m when Vijay's house casts a shadow 10m long on the ground. |
| At the same time, the tower casts a shadow 50 m long on the ground and the house of Ajay casts 20 m shadow on the ground. |
 |
| Based on the above information, answer the following questions |
What is the height of the tower?
A)
20m done
clear
B)
50m done
clear
C)
100m done
clear
D)
200m done
clear
View Solution play_arrow
-
question_answer2)
What will be the length of the shadow of the tower when Vijay's house casts a shadow of 12 m?
A)
75m done
clear
B)
50m done
clear
C)
45m done
clear
D)
60 done
clear
View Solution play_arrow
-
question_answer3)
What is the height of Ajay's house?
A)
30m done
clear
B)
40m done
clear
C)
50m done
clear
D)
20m done
clear
View Solution play_arrow
-
question_answer4)
When the tower casts a shadow of 40 m, same time what will be the length of the shadow of Ajay's house?
A)
16m done
clear
B)
32m done
clear
C)
20m done
clear
D)
8m done
clear
View Solution play_arrow
-
question_answer5)
When the tower casts a shadow of 40 m, same time what will be the length of the shadow of Vijay's house?
A)
15m done
clear
B)
32m done
clear
C)
16m done
clear
D)
8m done
clear
View Solution play_arrow
-
question_answer6)
| Directions: Q. 6 to 10 |
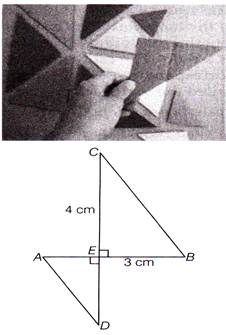
| Aashi wants to make a toran for Home using some pieces of cardboard. She cuts some cardboard pieces as shown below. If perimeter of \[\Delta ADE\] and \[\Delta BCE\] are in the ratio 4:3, then answer the following questions. |
 |
| Based on the above information, answer the following questions |
If the two triangles here are similar by SAS similarity rule, then their corresponding proportional sides are
A)
\[\frac{AE}{CE}=\frac{DE}{BE}\] done
clear
B)
\[\frac{BE}{AE}=\frac{CE}{DE}\] done
clear
C)
\[\frac{AD}{CE}=\frac{BE}{DE}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer7)
Length of BC =
A)
20/3 cm done
clear
B)
4 cm done
clear
C)
5cm done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer8)
Length of AD =
A)
10/3cm done
clear
B)
9/4cm done
clear
C)
5/3cm done
clear
D)
20/3cm done
clear
View Solution play_arrow
-
question_answer9)
Length of ED =
A)
4/3 cm done
clear
B)
8/3 cm done
clear
C)
7/3 cm done
clear
D)
16/3 cm done
clear
View Solution play_arrow
-
question_answer10)
Length of AE =
A)
\[\frac{2}{3}\times BE\] done
clear
B)
\[\sqrt{A{{D}^{2}}-D{{E}^{2}}}\] done
clear
C)
\[\frac{4}{3}\times \sqrt{B{{C}^{2}}-C{{E}^{2}}}\] done
clear
D)
AII of these done
clear
View Solution play_arrow
-
question_answer11)
| Directions: Q. 11 to 15 |
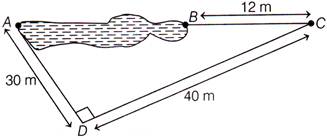
| Rohan wants to measure the distance of a pond during the visit to his native. He marks points A and B on the opposite edges of a pond as shown in the figure below. To find the distance between the points, he makes a right-angled triangle using rope connecting B with another point C are a distance of 12 m, connecting C to point D at a distance of 40 m from point C and the connecting D to the point A which at distance of 30 m from D such that \[\angle ADC=90{}^\circ \]. |
 |
| Based on the above information, answer the following questions |
| (i) Which property of geometry will be used to find the distance AC ? |
A)
Similarity of triangles done
clear
B)
Thales Theorem done
clear
C)
Pythagoras Theorem done
clear
D)
Area of similar triangles done
clear
View Solution play_arrow
-
question_answer12)
What is the distance AC ?
A)
50m done
clear
B)
12m done
clear
C)
100m done
clear
D)
70m done
clear
View Solution play_arrow
-
question_answer13)
Which is the following does not form a Pythagoras triplet?
A)
(7, 24, 25) done
clear
B)
(15, 8, 17) done
clear
C)
(5, 12, 13) done
clear
D)
(21, 20, 28) done
clear
View Solution play_arrow
-
question_answer14)
Find the length AS?
A)
12m done
clear
B)
38m done
clear
C)
50m done
clear
D)
100m done
clear
View Solution play_arrow
-
question_answer15)
Find the length of the rope used.
A)
120m done
clear
B)
70m done
clear
C)
82m done
clear
D)
22m done
clear
View Solution play_arrow
-
question_answer16)
| Directions: Q. 16 to 20 |
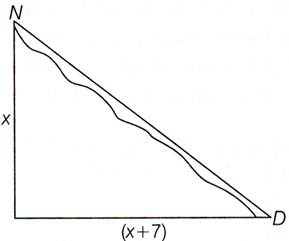
| D.M of a district went to town Noida from city Delhi. There is a route via town Ghaziabad such that \[NG\bot GD\], NG = x km and GD = (x + 7) km. He noticed that there is proposal to construct a 17 km highway which directly connects the two towns Noida and Delhi. |
 |
| Based on the above information, answer the following questions. |
| (i) Which concept can be used to get the value of x |
A)
Thales theorem done
clear
B)
Pythagoras theorem done
clear
C)
Converse of thales theorem done
clear
D)
Converse of Pythagoras theorem done
clear
View Solution play_arrow
-
question_answer17)
The value of x is
A)
4 done
clear
B)
6 done
clear
C)
5 done
clear
D)
8 done
clear
View Solution play_arrow
-
question_answer18)
The value of NG is
A)
10 km done
clear
B)
20km done
clear
C)
8km done
clear
D)
25km done
clear
View Solution play_arrow
-
question_answer19)
The value of GD is
A)
12km done
clear
B)
24km done
clear
C)
16km done
clear
D)
15km done
clear
View Solution play_arrow
-
question_answer20)
How much distance will be saved in reaching city Delhi after the construction of highway?
A)
6km done
clear
B)
9km done
clear
C)
4km done
clear
D)
8km done
clear
View Solution play_arrow
-
question_answer21)
| Directions: Q. 21 to 25 |
| A scale drawing of an object is the same shape at the object but a different size. |
| The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The scale is written as a ratio. The ratio of two corresponding sides in similar figures is called the scale fact |
| Scale factor = length in image/ corresponding length in object |
| If one shape can become another using revising, then the shapes are similar. |
| Hence, two shapes are similar when one can become the other after a resize, flip, slide or turn. In the photograph below showing the side view of a train engine. Scale factor is 1 : 200. |
 |
| This means that a length of 1 cm on the photograph above corresponds to a length of 200 cm or 2 m, of the actual engine. The scale can also be written as the ratio of two lengths. |
| Based on the above information, answer the following questions |
If the length of the model is 11 cm, then the overall length of the engine in the photograph above, including the couplings (mechanism used to connect) is
A)
22 cm done
clear
B)
220cm done
clear
C)
220m done
clear
D)
22m done
clear
View Solution play_arrow
-
question_answer22)
What will affect the similarity of any two polygons?
A)
They are flipped horizontally done
clear
B)
They are dilated by a scale factor done
clear
C)
They are translated down done
clear
D)
They are not the mirror image of one another. done
clear
View Solution play_arrow
-
question_answer23)
What is the actual width of the door, if the width of the door in photograph is 0.35 cm?
A)
0.7m done
clear
B)
0.7 cm done
clear
C)
0.07cm done
clear
D)
0.07m done
clear
View Solution play_arrow
-
question_answer24)
If two similar triangles have a scale factor 5 : 3 which statement regarding the two triangles is true?
A)
The ratio of their perimeters is 15 :1 done
clear
B)
Their altitudes have a ratio 25 :15 done
clear
C)
Their medians have a ratio 10 : 4 done
clear
D)
Their angle bisectors have a ration : 5 done
clear
View Solution play_arrow
-
question_answer25)
(v) The length of AB in the given figure
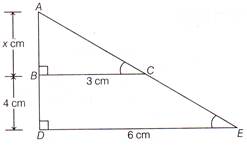
A)
8 cm done
clear
B)
6cm done
clear
C)
4cm done
clear
D)
10 cm done
clear
View Solution play_arrow
-
question_answer26)
| Directions: Q. 26 to 30 |
| Application of Pythagoras Theorem |
| A crow leaves a tree and flies due north at a speed of 600 km/h. At the same time, another crow leaves the same place and flies due west at the speed 800 km/h as shown below. After \[3\frac{1}{2}\]h both the crow reaches at point P and Q respectively. |
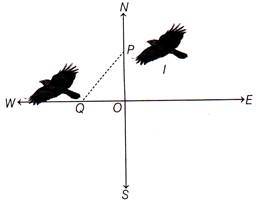 |
| Based on the above information, answer the following questions. |
Distance travelled by crow towards north after \[3\frac{1}{2}\] h is.
A)
1800km done
clear
B)
1500km done
clear
C)
1400km done
clear
D)
2100km done
clear
View Solution play_arrow
-
question_answer27)
Distance travelled by crow towards west after \[3\frac{1}{2}\] h is
A)
1600km done
clear
B)
2800km done
clear
C)
2250 km done
clear
D)
2625 km done
clear
View Solution play_arrow
-
question_answer28)
In the given figure, \[\angle POQ\] is
A)
\[70{}^\circ \] done
clear
B)
\[90{}^\circ \] done
clear
C)
\[80{}^\circ \] done
clear
D)
\[100{}^\circ \] done
clear
View Solution play_arrow
-
question_answer29)
Distance between crow after \[3\frac{1}{2}\] h is
A)
\[450\sqrt{41}\,km\] done
clear
B)
\[3500\,km\] done
clear
C)
\[125\sqrt{12}\,km\] done
clear
D)
\[472\,\sqrt{41}\,km\] done
clear
View Solution play_arrow
-
question_answer30)
Area of \[\Delta POQ\] is
A)
\[2940000k{{m}^{2}}\] done
clear
B)
\[179000k{{m}^{2}}\] done
clear
C)
\[186000k{{m}^{2}}\] done
clear
D)
\[2025000k{{m}^{2}}\] done
clear
View Solution play_arrow

