-
question_answer1)
| Directions: (1 - 5) |
| Let \[f\text{ }\left( x \right)\]be a real valued function, then its |
| Left Hand Derivative (L.H.D.) : |
| \[Lf'\left( a \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( a-h \right)-f\left( a \right)}{-h}\] |
| Right Hand Derivative (R.H.D.) : |
| \[Rf'\left( a \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( a+h \right)-f\left( a \right)}{h}\] |
| Also, a function \[f\left( x \right)\]is said to be differentiable at x = a if its L.H.D. and R.H.D. at x = a exist and are equal. |
For the function  answer the following questions answer the following questions |
R.H.D. of \[f\left( x \right)\] at \[x=1\] is
A)
1 done
clear
B)
-1 done
clear
C)
0 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer2)
L.H.D. of \[f\left( x \right)\] at \[x=1\] is
A)
1 done
clear
B)
-1 done
clear
C)
0 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer3)
\[f\left( x \right)\] is non-differentiable at
A)
x = 1 done
clear
B)
x = 2 done
clear
C)
x = 3 done
clear
D)
x = 4 done
clear
View Solution play_arrow
-
question_answer4)
Find the value of\[f'\left( 2 \right)\]
A)
1 done
clear
B)
2 done
clear
C)
3 done
clear
D)
-1 done
clear
View Solution play_arrow
-
question_answer5)
The value of f''(-1) is
A)
2 done
clear
B)
1 done
clear
C)
-2 done
clear
D)
-1 done
clear
View Solution play_arrow
-
question_answer6)
| Directions: (6 - 10) |
| Let \[f\left( x \right)\text{ }=\text{ }f\left( t \right)\] and \[y=g\left( t \right)\] be parametric forms with t as a parameter, then \[\frac{dy}{dx}=\frac{dy}{dt}\times \frac{dt}{dx}=\frac{g'\left( t \right)}{f'\left( t \right)}\], where \[f'\left( t \right)\ne 0\]. |
| On the basis of above information, answer the following questions. |
The derivative of \[f\left( \tan \,x \right)\]w.r.t. \[g\left( sec\text{ }x \right)\]at \[x=\frac{\pi }{4}\], where \[f'\left( 1 \right)=2\] and \[g'\left( \sqrt{2} \right)=4\], is
A)
\[\frac{1}{\sqrt{2}}\] done
clear
B)
\[\sqrt{2}\] done
clear
C)
1 done
clear
D)
0 done
clear
View Solution play_arrow
-
question_answer7)
The derivative of \[{{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right)\]with respect to \[{{\cos }^{-1}}\left( \frac{1-{{x}^{2}}}{1+{{x}^{2}}} \right)\] is
A)
- 1 done
clear
B)
1 done
clear
C)
2 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer8)
The derivative of \[{{e}^{{{x}^{3}}}}\]with respect to log x is
A)
\[{{e}^{{{x}^{3}}}}\] done
clear
B)
\[3{{x}^{2}}\,2{{e}^{{{x}^{3}}}}\] done
clear
C)
\[3{{x}^{3}}{{e}^{{{x}^{3}}}}\] done
clear
D)
\[3{{x}^{2}}{{e}^{{{x}^{3}}}}+3x\] done
clear
View Solution play_arrow
-
question_answer9)
The derivative of \[{{\cos }^{-1}}\left( 2x-1 \right)\]w.r.t. \[{{\cos }^{-1}}x\]is
A)
2 done
clear
B)
\[\frac{-1}{2\sqrt{1-{{x}^{2}}}}\] done
clear
C)
\[\frac{2}{x}\] done
clear
D)
\[1-{{x}^{2}}\] done
clear
View Solution play_arrow
-
question_answer10)
If \[y=\frac{1}{4}\,{{u}^{4}}\] and \[u=\frac{2}{3}\,{{x}^{3}}+5\], then \[\frac{dy}{dx}=\]
A)
\[\frac{2}{27}{{x}^{2}}{{\left( 2{{x}^{3}}+15 \right)}^{3}}\] done
clear
B)
\[\frac{2}{27}{{x}^{2}}{{\left( 2{{x}^{3}}+15 \right)}^{3}}\] done
clear
C)
\[\frac{2}{27}x{{\left( 2{{x}^{3}}+5 \right)}^{3}}\] done
clear
D)
\[\frac{2}{27}{{\left( 2{{x}^{3}}+15 \right)}^{3}}\] done
clear
View Solution play_arrow
-
question_answer11)
| Directions: (11 - 15) |
| Let \[f\,\,:\,\,A\to B\] and \[g\,\,:\,\,B\to C\] be two functions defined on non-empty sets A, B, C, then gof : \[A\to C\] be is called the composition of f and g defined as, \[gof\left( x \right)=\,g\left\{ f\left( x \right) \right\}\forall x\in A\]. |
Consider the funciton 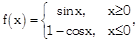 \[g\left( x \right)={{e}^{x}}\] and then answer the following questions. \[g\left( x \right)={{e}^{x}}\] and then answer the following questions. |
The function \[gof\left( x \right)\] is defined as
A)
B)
C)
D)
View Solution play_arrow
-
question_answer12)
\[\frac{d}{dx}\left\{ gof\left( x \right) \right\}=\]
A)
B)
C)
D)
View Solution play_arrow
-
question_answer13)
R.H.D. of \[gof\left( x \right)\]at x = 0 is
A)
0 done
clear
B)
1 done
clear
C)
-1 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer14)
L.H.D. of \[gof\left( x \right)\]at x = 0 is
A)
0 done
clear
B)
1 done
clear
C)
- 1 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer15)
The value of \[f'\left( x \right)\]at \[x=\frac{\pi }{4}\] is
A)
1/9 done
clear
B)
\[1/\sqrt{2}\] done
clear
C)
1/2 done
clear
D)
not defined done
clear
View Solution play_arrow
-
question_answer16)
| Directions: (16 - 20) |
| If a real valued function \[f\left( x \right)\]is finitely derivable at any point of its domain, it is necessarily continuous at that point. But its converse need not be true. |
| For example, every polynomial, constant function are both continuous as well as differentiable and inverse trigonometric functions are continuous and differentiable in its domains etc. |
| Based on the above information, answer the following questions. |
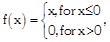
then at x = 0
A)
\[f\left( x \right)\] is differentiable and continuous done
clear
B)
\[f\left( x \right)\] is neither continuous nor differentiable done
clear
C)
\[f\left( x \right)\] is continuous but not differentiable done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer17)
If \[f\left( x \right)=\left| x-1 \right|,\,\,x\in R\], then at x=1
A)
\[f\left( x \right)\]is not continuous done
clear
B)
\[f\left( x \right)\] is continuous but not differentiable done
clear
C)
\[f\left( x \right)\] is continuous and differentiable done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer18)
\[f\left( x \right)={{x}^{3}}\] is
A)
continuous but not differentiable at x = 3 done
clear
B)
continuous and differentiable at x = 3 done
clear
C)
neither continuous nor differentiable at x = 3 done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer19)
If \[f\left( x \right)=\left[ sin\text{ }x \right]\], then which of the following is true?
A)
\[f\left( x \right)\]is continuous and differentiable at x = 0. done
clear
B)
\[f\left( x \right)\]is discontinuous at x = 0 done
clear
C)
\[f\left( x \right)\]is discontinuous at x = 0 but not differentiable. done
clear
D)
\[f\left( x \right)\] is differentiable but not continuous at \[x=\pi /2\]. done
clear
View Solution play_arrow
-
question_answer20)
If\[f\left( x \right)={{\sin }^{-1}}x,\,-1\,\le \,x\,\le \,\,1\], then
A)
\[f\left( x \right)\] is both continuous and differentiable done
clear
B)
\[f\left( x \right)\] is neither continuous nor differentiable. done
clear
C)
\[f\left( x \right)\] is continuous but not differentiable. done
clear
D)
None of these. done
clear
View Solution play_arrow
-
question_answer21)
| Directions: (21 - 25) |
| Derivative of \[y\text{ }=\text{ }f\left( x \right)\]w.r.t. x (if exists) is denoted by \[\frac{dy}{dx}\] of \[f'\left( x \right)\]and is called the first order derivative of y. |
| If we take derivative of again, then we get \[\frac{dy}{dx}\left( \frac{dy}{dx} \right)=\frac{{{d}^{2}}y}{d{{x}^{2}}}\] or \[f''\left( x \right)\] and is called the second order derivative of y. Similarly, \[\frac{d}{dx}\left( \frac{{{d}^{2}}y}{d{{x}^{2}}} \right)\] is denoted and defined as \[\frac{{{d}^{3}}y}{d{{x}^{3}}}\]or \[f'''\left( x \right)\] and is known as third order derivative of y and so on. |
| Based on the above information, answer the following questions. |
If \[y={{\tan }^{-1}}\left( \frac{\log \left( e/{{x}^{2}} \right)}{\log \left( e{{x}^{2}} \right)} \right)+{{\tan }^{-1}}\left( \frac{3+2\log \,x}{1-6\log \,x} \right)\], then \[\frac{{{d}^{2}}y}{d{{s}^{2}}}\]is equal to
A)
2 done
clear
B)
1 done
clear
C)
0 done
clear
D)
-1 done
clear
View Solution play_arrow
-
question_answer22)
If \[u={{x}^{2}}+{{y}^{2}}\] and \[x=s+3t\], \[y=2s-t\], then \[\frac{{{d}^{2}}u}{d{{s}^{2}}}\] is equal to
A)
12 done
clear
B)
32 done
clear
C)
36 done
clear
D)
10 done
clear
View Solution play_arrow
-
question_answer23)
\[f\left( x \right)=2\,\,\log \,\,\sin \,x\], then \[f''\left( x \right)\] is equal to
A)
\[2\,\,\cos e{{c}^{3}}\,x\] done
clear
B)
\[2\,{{\cot }^{2}}x-4{{x}^{2}}\,\cos e{{c}^{2}}\,{{x}^{2}}\] done
clear
C)
\[2x\,\cot \,{{x}^{2}}\] done
clear
D)
\[-2\,\cos e{{c}^{2}}\,x\] done
clear
View Solution play_arrow
-
question_answer24)
If \[f\left( x \right)={{e}^{x}}\,\sin \,x\], then \[f'''\left( x \right)=\]
A)
\[2{{e}^{x}}\left( \sin \,x+\cos \,x \right)\] done
clear
B)
\[2{{e}^{x}}\left( \cos x-\sin x \right)\] done
clear
C)
\[2{{e}^{x}}\left( \sin \,x-\cos \,x \right)\] done
clear
D)
\[2{{e}^{x}}\,\cos x\] done
clear
View Solution play_arrow
-
question_answer25)
If \[{{y}^{2}}=a{{x}^{2}}+bx+c\], then \[\frac{d}{dx}\left( {{y}^{3}}{{y}_{2}} \right)=\]
A)
1 done
clear
B)
-1 done
clear
C)
\[\frac{4ac-{{b}^{2}}}{{{a}^{2}}}\] done
clear
D)
0 done
clear
View Solution play_arrow
-
question_answer26)
| Directions: (26 - 30) |
| Logarithmic differentiation is a powerful technique to differentiate functions of the form \[f\left( x \right)={{\left[ u\left( x \right) \right]}^{v\left( x \right)}}\], where both u(x) and v(x) are differentiable functions and f and u need to be positive functions. |
| Let function \[y=f\left( x \right)={{\left( u\left( x \right) \right)}^{v\left( x \right)}}\], then |
| \[y'=y\left[ \frac{v(x)}{u(x)}u'(x)+v'(x)\centerdot log[u(x)] \right]\] |
| On the basis of above information, answer the following questions. |
Differentiate \[{{x}^{x}}\] w.r.t. x
A)
\[{{x}^{x}}\left( 1+\log \,x \right)\] done
clear
B)
\[{{x}^{x}}\left( 1-\log \,x \right)\] done
clear
C)
\[-{{x}^{x}}\left( 1+\log \,x \right)\] done
clear
D)
\[{{x}^{x}}\,\log \,x\] done
clear
View Solution play_arrow
-
question_answer27)
Differentiate \[{{x}^{x}}+{{a}^{x}}+{{x}^{a}}+{{a}^{a}}\] w.r.t. x
A)
\[\left( 1+\log \,x \right)+\left( {{a}^{x}}\,\log \,a+a{{x}^{a-1}} \right)\] done
clear
B)
\[{{x}^{x}}\left( 1+\log \,x \right)+\log \,a+a{{x}^{a-1}}\] done
clear
C)
\[{{x}^{x}}\left( 1+\log \,x \right)+{{x}^{a}}\,\operatorname{logx}+a{{x}^{a-1}}\] done
clear
D)
\[{{x}^{x}}\left( 1+\log \,x \right)+{{a}^{x}}\,\log \,a\,+\,a{{x}^{a-1}}\] done
clear
View Solution play_arrow
-
question_answer28)
If \[x={{e}^{x/y}}\], then find \[\frac{dy}{dx}\].
A)
\[-\frac{\left( x+y \right)}{x\,\log \,x}\] done
clear
B)
\[-\frac{\left( x-y \right)}{x\,\log \,x}\] done
clear
C)
\[\frac{\left( x+y \right)}{x\,\log \,x}\] done
clear
D)
\[\frac{\left( x-y \right)}{x\,\log \,x}\] done
clear
View Solution play_arrow
-
question_answer29)
If \[y={{\left( 2-x \right)}^{3}}\,{{\left( 3+2x \right)}^{5}}\], then find \[\frac{dy}{dx}\].
A)
\[{{\left( 2-x \right)}^{3}}{{\left( 3+2x \right)}^{5}}\left[ \frac{15}{3+2x}-\frac{8}{2-x} \right]\] done
clear
B)
\[{{\left( 2-x \right)}^{3}}{{\left( 3+2x \right)}^{5}}\left[ \frac{15}{3+2x}+\frac{3}{2-x} \right]\] done
clear
C)
\[{{\left( 2-x \right)}^{3}}{{\left( 3+2x \right)}^{5}}\left[ \frac{10}{3+2x}-\frac{3}{2-x} \right]\] done
clear
D)
\[{{\left( 2-x \right)}^{3}}{{\left( 3+2x \right)}^{5}}\left[ \frac{10}{3+2x}+\frac{3}{2-x} \right]\] done
clear
View Solution play_arrow
-
question_answer30)
If \[y={{x}^{x}}\,\,{{e}^{\left( 2x+5 \right)}}\] , then \[\frac{dy}{dx}\]is
A)
\[{{x}^{x}}{{e}^{\left( 2x+5 \right)}}\,\left( 2+\log \,\,x \right)\] done
clear
B)
\[{{x}^{x}}{{e}^{\left( 2x+5 \right)}}\,\left( 3+2\,\log \,x \right)\] done
clear
C)
\[{{x}^{x}}\,{{e}^{\left( 2x+5 \right)}}\,\,\left( 2+3\,\log \,x \right)\] done
clear
D)
\[{{x}^{x}}\,{{e}^{\left( 2x+5 \right)}}\,\left( 3+\log \,x \right)\] done
clear
View Solution play_arrow
-
question_answer31)
| Directions: (31 - 35) |
| If \[y=f\left( u \right)\]is a differentiable function of u and \[u=g\left( x \right)\]is a differentiable function of x, then \[y=f\left[ \left( g\left( x \right) \right. \right]\]is a differentiable function of x and\[\frac{dy}{dx}=\frac{dy}{du}\times \frac{du}{dx}\]. This rule is also known as CHAIN RULE. |
| Based on the above information, find the derivative of functions w.r.t. x in the following questions. |
\[\cos \sqrt{x}\]
A)
\[\frac{-\sin \sqrt{x}}{2\sqrt{x}}\] done
clear
B)
\[\frac{\sin \sqrt{x}}{-\sin \sqrt{x}}\] done
clear
C)
\[sin\sqrt{x}\] done
clear
D)
\[-\sin \sqrt{x}\] done
clear
View Solution play_arrow
-
question_answer32)
\[{{7}^{x+\frac{1}{x}}}\]
A)
\[\left( \frac{{{x}^{2}}-1}{{{x}^{2}}} \right)\centerdot {{7}^{x+\frac{1}{x}}}\centerdot \log 7\] done
clear
B)
\[\left( \frac{{{x}^{2}}+1}{{{x}^{2}}} \right)\centerdot {{7}^{x+\frac{1}{x}}}\centerdot \log 7\] done
clear
C)
\[\left( \frac{{{x}^{2}}-1}{{{x}^{2}}} \right)\centerdot {{7}^{x-\frac{1}{x}}}\centerdot \log 7\] done
clear
D)
\[\left( \frac{{{x}^{2}}+1}{{{x}^{2}}} \right)\centerdot {{7}^{x+\frac{1}{x}}}\centerdot \log 7\] done
clear
View Solution play_arrow
-
question_answer33)
\[\sqrt{\frac{1-\cos x}{1+\cos \,x}}\]
A)
\[\frac{1}{2}{{\sec }^{2}}\frac{x}{2}\] done
clear
B)
\[-\frac{1}{2}{{\sec }^{2}}\frac{x}{2}\] done
clear
C)
\[{{\sec }^{2}}\frac{x}{2}\] done
clear
D)
\[-{{\sec }^{2}}\frac{x}{2}\] done
clear
View Solution play_arrow
-
question_answer34)
\[\frac{1}{b}{{\tan }^{-1}}\left( \frac{x}{b} \right)+\frac{1}{a}{{\tan }^{-1}}\left( \frac{x}{a} \right)\]
A)
\[\frac{-1}{{{x}^{2}}+{{b}^{2}}}+\frac{1}{{{x}^{2}}+{{a}^{2}}}\] done
clear
B)
\[\frac{1}{{{x}^{2}}+{{b}^{2}}}+\frac{1}{{{x}^{2}}+{{a}^{2}}}\] done
clear
C)
\[\frac{1}{{{x}^{2}}+{{b}^{2}}}-\frac{1}{{{x}^{2}}+{{a}^{2}}}\] done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer35)
\[{{\sec }^{-1}}x+\cos e{{c}^{-1}}\frac{x}{\sqrt{{{x}^{2}}-1}}\]
A)
\[\frac{2}{\sqrt{{{x}^{2}}-1}}\] done
clear
B)
\[\frac{-2}{\sqrt{{{x}^{2}}-1}}\] done
clear
C)
\[\frac{1}{\left| x \right|\,\sqrt{{{x}^{2}}-1}}\] done
clear
D)
\[\frac{2}{\left| x \right|\,\sqrt{{{x}^{2}}-1}}\] done
clear
View Solution play_arrow
-
question_answer36)
| Directions: (36 - 40) |
| If a relation between x and y is such that y cannot be expressed in terms of x, then y is called an implicit function of x. When a given relation expresses y as an implicit function of x and we want to find \[\frac{dy}{dx}\], then we differentiate every term of the given relation w.r.t x, remembering that a term in y is first differentiated w.r.t. y and then multiplied by \[\frac{dy}{dx}\]. |
| Based on the above information, find the value of \[\frac{dy}{dx}\]in each of the following questions. |
\[{{x}^{3}}+{{x}^{2}}y+x{{y}^{2}}+{{y}^{3}}=81\]
A)
\[\frac{\left( 3{{x}^{2}}+2xy+{{y}^{2}} \right)}{{{x}^{2}}+2xy+3{{y}^{2}}}\] done
clear
B)
\[\frac{-\left( 3{{x}^{2}}+2xy+{{y}^{2}} \right)}{{{x}^{2}}+2xy+3{{y}^{2}}}\] done
clear
C)
\[\frac{\left( 3{{x}^{2}}+2xy-{{y}^{2}} \right)}{{{x}^{2}}-2xy+3{{y}^{2}}}\] done
clear
D)
\[\frac{3{{x}^{2}}+xy+{{y}^{2}}}{{{x}^{2}}+xy+3{{y}^{2}}}\] done
clear
View Solution play_arrow
-
question_answer37)
\[{{x}^{y}}={{e}^{x-y}}\]
A)
\[\frac{x-y}{\left( 1+\log \,x \right)}\] done
clear
B)
\[\frac{x+y}{\left( 1+\log \,x \right)}\] done
clear
C)
\[\frac{x-y}{x\left( 1+\log x \right)}\] done
clear
D)
\[\frac{x+y}{x\left( 1+\log \,x \right)}\] done
clear
View Solution play_arrow
-
question_answer38)
\[{{e}^{\sin \,y}}=xy\]
A)
\[\frac{-y}{x\,\left( y\,\cos y-1 \right)}\] done
clear
B)
\[\frac{y}{v\,\cos \,y-1}\] done
clear
C)
\[\frac{y}{y\,cos\,y+1}\] done
clear
D)
\[\frac{y}{x\left( y\,\cos y-1 \right)}\] done
clear
View Solution play_arrow
-
question_answer39)
\[{{\sin }^{2}}x+{{\cos }^{2}}y=1\]
A)
\[\frac{\sin \,2y}{\sin \,2x}\] done
clear
B)
\[-\frac{\sin \,2x}{\sin \,2y}\] done
clear
C)
\[-\frac{\sin \,2y}{\sin \,2x}\] done
clear
D)
\[\frac{\sin \,2y}{\sin \,2x}\] done
clear
View Solution play_arrow
-
question_answer40)
\[y={{\left( \sqrt{x} \right)}^{{{\sqrt{x}}^{\sqrt{x}....\infty }}}}\]
A)
\[\frac{-{{y}^{2}}}{x\left( 2-y\,\log \,x \right)}\] done
clear
B)
\[\frac{{{y}^{2}}}{2+y\,\log \,x}\] done
clear
C)
\[\frac{{{y}^{2}}}{x\left( 2+y\,\log \,x \right)}\] done
clear
D)
\[\frac{{{y}^{2}}}{x\left( 2-y\,\log \,x \right)}\] done
clear
View Solution play_arrow
