-
question_answer1)
| Directions: (1 - 8) |
| The following questions consist of two statements, one labelled as "Assertion [A] and the other labelled as Reason [R]" You are to examine these two statements carefully and decide if Assertion [A] and Reason [R] are individually true and if so, whether the Reason [R] is the correct explanation for the given Assertion [A]. Select your answer from following options. |
| |
| Consider the graph of constraints stated in linear equations \[5x+y\le 100\], \[y+x\le 60\], x, \[y\ge 0\]. |
| Assertion [A]: (25, 40) is in feasible solution of the problem. |
| Reason [R]: Any point inside the feasible region is called an infeasible solution. |
A)
Both A and R are individually true and R is the correct explanation of A. done
clear
B)
Both A and R are individually true and R is not the correct explanation of A. done
clear
C)
'A' is true but 'R' is false done
clear
D)
'A' is false but 'R' is true done
clear
E)
Both A and R are false done
clear
View Solution play_arrow
-
question_answer2)
| Assertion [A]: Maximum value of \[z=11x+5y\] subject to the constraints |
| \[3x+2y\le 25,\,x+y\,\le 10,\,x,\,y\ge 0\] occurs at corner point \[\left( \frac{25}{3},\,0 \right)\]. |
| Reason [R]: If the feasible region of the given LPP is bounded then the maximum & minimum value of the objective function occur at corner points. |
A)
Both A and R are individually true and R is the correct explanation of A. done
clear
B)
Both A and R are individually true and R is not the correct explanation of A. done
clear
C)
'A' is true but 'R' is false done
clear
D)
'A' is false but 'R' is true done
clear
E)
Both A and R are false done
clear
View Solution play_arrow
-
question_answer3)
| Assertion [A]: The maximum value of \[z=11x+7y\] subject to the constraints \[2x+y\le 6,\,x\le 2,\,y\ge 0,\,y\ge 0\] occurs at corner point (0, 6). |
| Reason [R]: If the feasible region of the given LPP is bounded then the minimum & maximum values of the objective function occurs at corner points. |
A)
Both A and R are individually true and R is the correct explanation of A. done
clear
B)
Both A and R are individually true and R is not the correct explanation of A. done
clear
C)
'A' is true but 'R' is false done
clear
D)
'A' is false but 'R' is true done
clear
E)
Both A and R are false done
clear
View Solution play_arrow
-
question_answer4)
| Assertion [A]: The maximum value of \[z=4x+y\] subject to the constraints \[x+y\le 50,\,3x+y\le 90,\]\[\,x\ge 0,\,y\ge 0\] is 120. |
| Reason [R]: If the feasible region of given LPP is bounded then the maximum & minimum values of the objective function occurs in infleasible region. |
A)
Both A and R are individually true and R is the correct explanation of A. done
clear
B)
Both A and R are individually true and R is not the correct explanation of A. done
clear
C)
'A' is true but 'R' is false done
clear
D)
'A' is false but 'R' is true done
clear
E)
Both A and R are false done
clear
View Solution play_arrow
-
question_answer5)
| Consider the graph of \[2x+3y\le 12\], \[3x+2y\le 12\], \[x\ge 0,\,y\,\ge 0\]. |
| Assertion [A]: (5, 1) is an infeasible solution of the problem. |
| Reason [R]: Any point inside the feasible region is called an infeasible solution. |
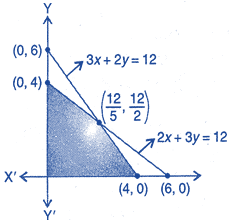 |
A)
Both A and R are individually true and R is the correct explanation of A. done
clear
B)
Both A and R are individually true and R is not the correct explanation of A. done
clear
C)
'A' is true but 'R' is false done
clear
D)
'A' is false but 'R' is true done
clear
E)
Both A and R are false done
clear
View Solution play_arrow
-
question_answer6)
| Consider the graph of constraints |
| \[x+y\le 24,\,2x+y\le 32,\,x>0,\,y>0\] |
| Assertion [A]: The points (16, 0), (8, 16) and (0, 24) are feasible solutions. |
| Reason [R]: Points within and on the boundary of the feasible region represents feasible solutions of the constraints. |
A)
Both A and R are individually true and R is the correct explanation of A. done
clear
B)
Both A and R are individually true and R is not the correct explanation of A. done
clear
C)
'A' is true but 'R' is false done
clear
D)
'A' is false but 'R' is true done
clear
E)
Both A and R are false done
clear
View Solution play_arrow
-
question_answer7)
| Consider the graph of linear equations \[x+y\le 4,\,x,\,y\,\ge 0\] |
| Assertion [A]: (5, 1) is a feasible solution of the problem |
| Reason [R]: Any point inside the feasible region is called feasible solution. |
A)
Both A and R are individually true and R is the correct explanation of A. done
clear
B)
Both A and R are individually true and R is not the correct explanation of A. done
clear
C)
'A' is true but 'R' is false done
clear
D)
'A' is false but 'R' is true done
clear
E)
Both A and R are false done
clear
View Solution play_arrow
-
question_answer8)
| Consider the graph of constraints |
| \[5x+y\le 100,\,x+y\,\le 60,\,x,\,y\,\ge 0\] |
| Assertion [A]: The points (10, 50), (0, 60) and (20, 0) are feasible solutions. |
| Reason [R]: Points within and on the boundary of the feasible region represents infeasible solutions. |
A)
Both A and R are individually true and R is the correct explanation of A. done
clear
B)
Both A and R are individually true and R is not the correct explanation of A. done
clear
C)
'A' is true but 'R' is false done
clear
D)
'A' is false but 'R' is true done
clear
E)
Both A and R are false done
clear
View Solution play_arrow
