-
question_answer1)
| Directions: (1 - 5) |
| Linear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations. |
| Based on the above information, answer the following questions : |
The optimal value of the objective function is attained at the points
A)
on X-axis done
clear
B)
on Y-axis done
clear
C)
which are corner points of the feasible region done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer2)
The graph of the inequality \[3x+\text{4}y<12\] is
A)
half plane that contains the origin done
clear
B)
half plane that neither contains the origin nor the points of the line \[3x+4y=12\]. done
clear
C)
Whole XOY-plane excluding the points on line \[3x+4y=12\] done
clear
D)
None of these. done
clear
View Solution play_arrow
-
question_answer3)
| The feasible region for an LPP is shown in the figure. Let \[Z=2x+5y\] be the objective function. Maximum of Z occurs at |
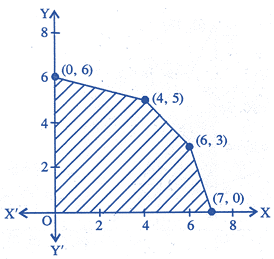 |
A)
(7, 0) done
clear
B)
(6, 3) done
clear
C)
(0, 6) done
clear
D)
(4, 5) done
clear
View Solution play_arrow
-
question_answer4)
The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20). Let \[Z\text{ }=\text{ }px\text{ }+\text{ }qy\], where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is
A)
p = q done
clear
B)
p = 2q done
clear
C)
q = 2p done
clear
D)
q = 3p done
clear
View Solution play_arrow
-
question_answer5)
| The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y. |
| Compare the quantity in Column A and Column B. |
| Column A | Column B |
| Maximum of Z | 325 |
A)
The quantity in column A is greater done
clear
B)
The quantity in column B is greater done
clear
C)
The two quantities are equal done
clear
D)
The relationship cannot be determined on the basis of the information supplied. done
clear
View Solution play_arrow
-
question_answer6)
| Directions: (6 - 10) |
| Deepa rides her car at 25 km/hr. She has to spend Rs 2 per km on diesel and if she rides it at a faster speed of 40 km/her, the diesel cost increases to Rs 5 per km. She has Rs 100 to spend on diesel. Let she travels x kms with speed 25 km/h and y kms with speed 40 km/hr. The feasible region for the LPP is shown below : |
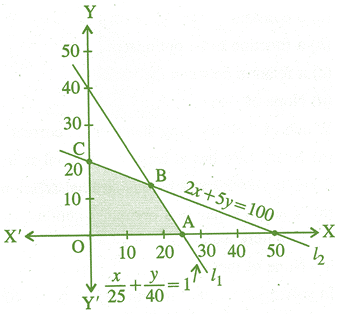 |
| Based on the above information, answer the following questions : |
What is the point of intersection of line \[{{l}_{1}}\]and \[{{l}_{2}}\]?
A)
\[\left( \frac{40}{3},\frac{50}{3} \right)\] done
clear
B)
\[\left( \frac{50}{3},\frac{40}{3} \right)\] done
clear
C)
\[\left( \frac{-50}{3},\frac{40}{3} \right)\] done
clear
D)
\[\left( \frac{-50}{3},\frac{-40}{3} \right)\] done
clear
View Solution play_arrow
-
question_answer7)
The corner points of the feasible region shown in above graph are
A)
\[\left( 0,25 \right)\text{, (20,0)}\left( \frac{40}{3},\frac{50}{3} \right)\text{ }\] done
clear
B)
\[\left( 0,0 \right)\text{, (25,0), (0,20)}\] done
clear
C)
\[\left( 0,0 \right)\text{, }\left( \frac{40}{3},\frac{50}{3} \right),(0,20)\] done
clear
D)
\[\left( 0,0 \right)\text{, (25,0),}\left( \frac{50}{3},\frac{40}{3} \right),(0,20)\] done
clear
View Solution play_arrow
-
question_answer8)
If \[Z=x+y\] be the objective function and max Z = 30. Then maximum value occurs at point
A)
\[\left( \frac{50}{3},\frac{40}{3} \right)\] done
clear
B)
\[(0,0)\] done
clear
C)
(25,0) done
clear
D)
(0,20) done
clear
View Solution play_arrow
-
question_answer9)
If \[Z=6x-9y\] be the objective function, then maximum value of Z is
A)
-20 done
clear
B)
150 done
clear
C)
180 done
clear
D)
20 done
clear
View Solution play_arrow
-
question_answer10)
If Z = 6x + 3y be the objective function, then what is the minimum value of Z?
A)
120 done
clear
B)
130 done
clear
C)
0 done
clear
D)
150 done
clear
View Solution play_arrow
-
question_answer11)
| Directions: (11 - 15) |
| Corner points of the feasible region for an LPP are (0, 3), (5, 0), (6, 8), (0, 8). Let \[Z\text{ }=4x-6y\] be the objective function. |
| Based on the above information, answer the following questions: |
The minimum value of Z occurs at
A)
(6, 8) done
clear
B)
(5, 0) done
clear
C)
(0,3) done
clear
D)
(0,8) done
clear
View Solution play_arrow
-
question_answer12)
Maximum value of Z occurs at
A)
(5,0) done
clear
B)
(0,8) done
clear
C)
(0, 3) done
clear
D)
(6, 8) done
clear
View Solution play_arrow
-
question_answer13)
Maximum of Z - Minimum of Z =
A)
58 done
clear
B)
68 done
clear
C)
78 done
clear
D)
88 done
clear
View Solution play_arrow
-
question_answer14)
The corner points of the feasible region determined by the system of linear inequalities are
A)
(0, 0), (-3, 0), (3, 2), (2, 3) done
clear
B)
(3, 0), (3, 2), (2, 3), (0, -3) done
clear
C)
(0, 0), (3, 0), (3, 2), (2, 3). (0, 3) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer15)
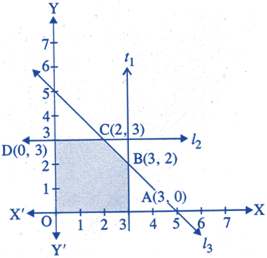 |
| The feasible solution of LPP belongs to |
A)
first and second quadrant done
clear
B)
first and third quadrant done
clear
C)
only second quadrant done
clear
D)
only first quadrant done
clear
View Solution play_arrow
-
question_answer16)
| Directions: (16 - 20) |
| Suppose a dealer in rural areas wishes to purpose a number of sewing machines. He has only Rs 5760 to invest and has space for at most 20 items for storage. |
| An electronic sewing machine costs him Rs 360 and a manually operated sweing mechine Rs 240. He can sell an electronic sewing machine at a profit of Rs 22 and a mutually operated sewing machine at a profit of Rs 18. |
| Based on the above information, answer the following questions : |
Let x and y denotes the number of electronic sewing machines and manually operated sewing machines purchased by the dealer. If it is assume that the dealer purchased at least one of the given machines, then
A)
\[x+y\ge 0\] done
clear
B)
\[x+y<0\] done
clear
C)
\[x+y>0\] done
clear
D)
\[x+y\le 0\] done
clear
View Solution play_arrow
-
question_answer17)
| Let the constraints in the given problem is represented by the following inequalities: |
| \[x\text{ }+\text{ }y\text{ }\le 20\] |
| \[360x+240y\le 5760\] |
| \[x,y\ge 0\] |
| Then which of the following point lie in its feasible region? |
A)
(0, 24) done
clear
B)
(8, 12) done
clear
C)
(20, 2) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer18)
If the objective function of the given problem is maximise \[z=22x+18y,\] then its optimal value occur at
A)
(0, 0) done
clear
B)
(16, 0) done
clear
C)
(8, 12) done
clear
D)
(0, 20) done
clear
View Solution play_arrow
-
question_answer19)
| Suppose the following shaded region APDO, represent the feasible region corresponding to mathematical formulation of given problem. |
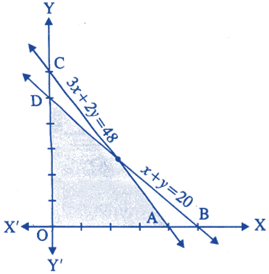 |
| Then which of the following represent the coordinates of one of its corner points ? |
A)
(0, 24) done
clear
B)
(12, 8) done
clear
C)
(8, 12) done
clear
D)
(6, 14) done
clear
View Solution play_arrow
-
question_answer20)
If an LPP admits optimal solution at two consecutive vertices of a feasible region, then
A)
the required optimal solution is at the mid-point of the line joining two points. done
clear
B)
the optimal solution occurs at every point on the line joining these two points. done
clear
C)
the LPP under consideration is not solvable. done
clear
D)
the LPP under consideration must reconstructed. done
clear
View Solution play_arrow
-
question_answer21)
| Directions: (21 - 25) |
| Let R be the feasible region (convex polygon) for a linear programming problem and let \[Z=ax+by\] be objective function. When Z has an optimal value (Maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region. |
| Based on the above information, answer the following questions: |
Objective function of a L.P.P. is
A)
a constant done
clear
B)
a function to be optimized done
clear
C)
a relation between the variables done
clear
D)
None of these. done
clear
View Solution play_arrow
-
question_answer22)
Which of the following statement is correct
A)
Every LPP has at least one optimal solution done
clear
B)
Every LPP has a unique optimal solution done
clear
C)
If an LPP has two optimal solutions, then it has infinitely many solutions done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer23)
In solving the LPP : minimise \[f=6x+10y\] subject to contraints \[x\ge 6,\text{ }y\ge 2,\text{ }2x+y\ge 10,\text{ }x\ge 10,\,\,y\ge 0\] reducdant constraints are
A)
\[x\ge 6,y\ge 2\] done
clear
B)
\[2x+y\ge 10,\,x\ge 0,\,\,y\ge 0\] done
clear
C)
\[x\ge 6\] done
clear
D)
None of these. done
clear
View Solution play_arrow
-
question_answer24)
| The feasible region for a LPP is shown in the figure. Let \[Z=3x-4y\] be the objective function Minimum of Z occur at |
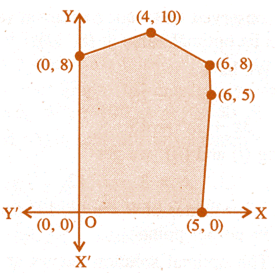 |
A)
(0, 0) done
clear
B)
(0, 8) done
clear
C)
(5, 0) done
clear
D)
(4, 10). done
clear
View Solution play_arrow
-
question_answer25)
| The feasible region for a LPP is shown shaded in the figure. Let \[F=3x-4y\] be the objective function. |
| Maximum value of F is |
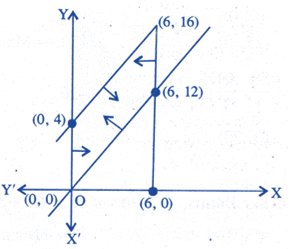 |
A)
0 done
clear
B)
8 done
clear
C)
12 done
clear
D)
18 done
clear
View Solution play_arrow

