12th Class Mathematics Relations and Functions Question Bank

done Assertion And Reason (MCQs) - Relations and Functions Total Questions - 13

• question_answer1)

  Directions: (1 - 13)

  The following questions consist of two statements, one labelled as "Assertion [A] and the other labelled as Reason [R]". You are to examine these two statements carefully and decide if Assertion [A] and Reason [R] are individually true and if so, whether the Reason [R] is the correct explanation for the given Assertion [A]. Select your answer from following options.

  Assertion: A relation R = {(1, 1), (1, 3), (3, 1), (3, 3), (3, 5)} defined on the set \[A=\left\{ 1,3,5 \right\}\]is reflexive.

  Reason: A relation R on the set A is said to be transitive if for. \[\left( a,\text{ }b \right)~\in R\] and \[\left( b,\text{ }c \right)\in R\], we have \[\left( a,\,c \right)\in R\].

   
  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer2)

  Assertion: A relation \[R=\left\{ \left( a,\,b \right)\,:\,\,|a-b|\,<\,2 \right\}\]defined on the set \[A=\left\{ 1,\,2,\,3,\,4,\,5 \right\}\] is reflexive.

  Reason: A relation R on the set A is said to be reflexive if for \[\left( a,\,b \right)\in \,R\] and\[\left( b,\,c \right)\in \,R\], we have \[\left( a,\,c \right)\in R\].

   
  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer3)

  Assertion: A relation \[R=\left\{ \left( x,\,y \right)\,\,:\,\,|\,x\,-\,y|\,=0 \right\}\] defined on the set A = {3, 5, 7} is symmetric.

  Reason: A relation R on the set A is said to be symmetric if for \[\left( a,\,\,b \right)\in R\], we have \[\left( b,\,\,a \right)\in R\].

   
  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer4)

  Assertion: The relation R in the set A = {1, 2, 3, 4, 5, 6} defined as R = {(x, y) : y is divisible by x} is an equivalence relation.

  Reason: A relation R on the set A is equivalence if it is reflexive, symmetric and transitive.

  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer5)

  Assertion: The relation R in set A of human beings in a town at a particular time given by :

  R = {(x, y) : x is exactly 5 years younger than y} is symmetric.

  Reason: A relation R on the set A is said to be symmetric if \[\left( a,\,\,b \right)\in R\] but \[\left( b,\,\,a \right)\notin R\].

   
  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer6)

  Assertion: A relation R = {(1, 1), (1, 2), (2, 2), (2, 3), (3, 3)} defined on the set A = {1, 2, 3} is reflexive.

  Reason: A relation R on the set A is said to be reflexive if \[\left( a,\,a \right)\in R\,\,for  all \,\,a\,\,\in \,\,A\].

   
  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer7)

  Assertion: A relation R = {(1, 1), (1, 2), (2, 2), (2, 3), (3, 3)} is symmetric

  Reason: A relation R on the set A is said to be symmetric if\[\left( a,\,\,b \right)\in R\], then\[\left( b,\,\,a \right)\in \,R\].

  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer8)

  Assertion: A relation R = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5)} defined on the set A = {1, 3, 5) is transitive.

  Reason: A relation R on the set A is said to be transitive if for \[\left( a,\text{ }b \right)\text{ }\in \,\,\text{R}\] and \[\left( a,\text{ c} \right)\text{ }\in \,\,\text{R}\], we have \[\left( b,\,\,c \right)\in \,\,R\].

   
  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer9)

  Assertion: Domain and Range of a relation

  \[R=\left\{ \left( x,\text{ }y \right):x-2y=0 \right\}\]defined on the set \[A=\left\{ 1,2,3,4 \right\}\]are respectively \[\left\{ 1,2,3,4 \right\}\]and\[\left\{ 2,4,6,8 \right\}\].

  Reason: Domain and Range of a relation R are respectively the sets \[\left\{ a\,\,\,:\,\,a\,\,\in A \right.\]and \[\left. \left( a,\,\,b \right)\,\,\in \,\,R \right\}\]and \[\left\{ b\,\,:\,\,b\,\,\in \,\,A\,and\,\,\left( a,\,\,b \right)\,\in \,R \right\}\]

  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer10)

  Assertion: The Greatest Integer Function \[f\,\,\,:\,\,\,R\to R\]given by \[f\left( x \right)=\left[ x \right]\]is not one-one.

  Reason: A function \[f\,\,:\,\,A\to B\] is said to injective if \[f\left( a \right)=f\left( b \right)\Rightarrow a=b\].

   
  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false.   done clear
  View Solution play_arrow

• question_answer11)

  Assertion: A mapping shown in the following figure is not surjective

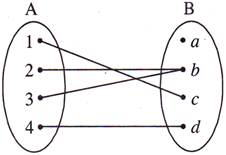  Reason: A function \[f\,\,:\,\,A\to B\] is said to be surjective if every element of B has a pre-image in A.

  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer12)

  Assertion: A function \[f\,\,:\,\,N\,\,\to N\]be defined by

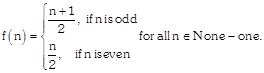  Reason: A function \[f\,\,:\,\,A\to B\]is said to be injective if \[f\left( a \right)=f\left( b \right)\Rightarrow a=b\].

  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow

• question_answer13)

  Assertion: A function \[f\,\,:\,\,Z\to Z\] defined as \[f\left( x \right)={{x}^{2}}\] is injective.

  Reason: A function \[f\,\,:\,\,A\to B\] is said to be injective if every element of B has a pre-image in A.

  A)
  Both A and R are individually true and R is the correct explanation of A. done clear
  B)
  Both A and R are individually true and R is not the correct explanation of A. done clear
  C)
  'A' is true but 'R' is false done clear
  D)
  'A' is false but 'R' is true done clear
  E)
  Both A and R are false. done clear
  View Solution play_arrow