9th Class Mathematics Lines and Angles Question Bank

done Lines and angles Total Questions - 30

• question_answer1)
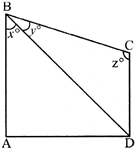
  In the given figure, \[\mathbf{AB}\parallel \mathbf{DC}\]. If \[\mathbf{x=}\frac{\mathbf{4}}{\mathbf{3}}\mathbf{y}\] and \[\mathbf{y=}\frac{\mathbf{3}}{\mathbf{5}}\mathbf{z}\], find the values of y.
  A)
   \[{{45}^{{}^\circ }}\]           done clear
  B)
   \[{{44}^{{}^\circ }}\] done clear
  C)
   \[{{36}^{{}^\circ }}\]                          done clear
  D)
   \[{{40}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer2)
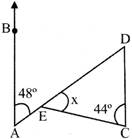
  Compute the value of x in the given figure if AB || DC,
  A)
   \[{{88}^{{}^\circ }}\]   done clear
  B)
   \[{{48}^{{}^\circ }}\] done clear
  C)
   \[{{118}^{{}^\circ }}\]                                   done clear
  D)
   \[{{108}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer3)
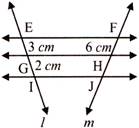
  In the given figure if parallel lines, EF, GFL, IJ are intersected by transversals. \[l\]and m. Where \[\mathbf{EG}=\mathbf{3}\text{ }\mathbf{cm},\mathbf{GI}=\mathbf{2}\text{ }\mathbf{cm},\text{ }\mathbf{FH}=\mathbf{6}\]cm, then HJ is
  A)
   8 cm                            done clear
  B)
   9cm done clear
  C)
   12cm                           done clear
  D)
   4cm done clear
  View Solution play_arrow

• question_answer4)
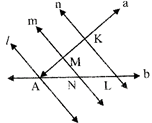
  In the given figure \[\ell \parallel m\parallel \mathbf{n}\] and transversals a and b through A intersects them at A, M, K, N, L. If AN = 6 cm, NL = 24 cm , KM = 32 cm, then the length of intercept AM is
  A)
   8 cm     done clear
  B)
   6 cm done clear
  C)
   12 cm                          done clear
  D)
   10 cm done clear
  View Solution play_arrow

• question_answer5)
  In the given figure \[\mathbf{AB}\parallel \mathbf{CD}\parallel \mathbf{EF}\]. If \[\mathbf{5x}=\mathbf{4y}\] and \[\mathbf{z}=\mathbf{y}+\mathbf{10}\], then the value of w is
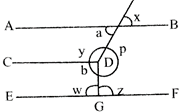
  A)
   \[{{60}^{{}^\circ }}\]                        done clear
  B)
   \[{{50}^{{}^\circ }}\] done clear
  C)
   \[{{90}^{{}^\circ }}\]                                    done clear
  D)
   \[{{70}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer6)
  If \[\mathbf{AB}\parallel \mathbf{CD},\mathbf{EF}\parallel \mathbf{GH}\], then the value of a, b, c.
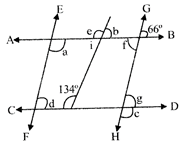
  A)
   \[a={{114}^{{}^\circ }},b={{46}^{{}^\circ }},c={{114}^{{}^\circ }}\]  done clear
  B)
   \[a={{104}^{{}^\circ }},b={{56}^{{}^\circ }},c={{114}^{{}^\circ }}\] done clear
  C)
   \[a={{114}^{{}^\circ }},b={{26}^{{}^\circ }},c={{154}^{{}^\circ }}\]        done clear
  D)
   \[a={{94}^{{}^\circ }},b={{46}^{{}^\circ }},c={{54}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer7)
  In the figure, \[\mathbf{AB}\parallel \mathbf{CD}.\]If \[\angle \mathbf{EAB}=\mathbf{4}{{\mathbf{5}}^{{}^\circ }}\]and \[\angle \mathbf{ECD}=\mathbf{5}{{\mathbf{5}}^{{}^\circ }}\], then \[\angle \mathbf{AEB}=\]?
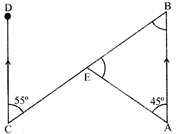
  A)
   \[{{50}^{{}^\circ }}\]                                    done clear
  B)
   \[{{60}^{{}^\circ }}\] done clear
  C)
   \[{{80}^{{}^\circ }}\]      done clear
  D)
   \[{{55}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer8)
  P and Q are points on the opposite sides of a straight line AB. If O is a point on AB such that\[\angle \mathbf{AOP}=\angle \mathbf{BOQ}\], then which one of the following is correct?
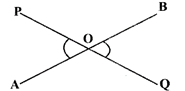
  A)
   \[\angle AOQ<\angle BOP\]        done clear
  B)
   \[\angle AOQ>\angle BOP\] done clear
  C)
   \[\angle AOP={{180}^{{}^\circ }}-\angle AOQ\]        done clear
  D)
   \[\angle AOP={{90}^{{}^\circ }}-\angle AOQ\] done clear
  View Solution play_arrow

• question_answer9)
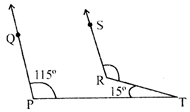
  In the given figure. If \[\mathbf{PQ}\parallel \mathbf{RS},\mathbf{ZQPT}=\mathbf{11}{{\mathbf{5}}^{{}^\circ }}\] and \[\angle \mathbf{PTR}=\mathbf{1}{{\mathbf{5}}^{{}^\circ }}\], then \[\angle \mathbf{SRT}\] is equal to:
  A)
   \[{{145}^{{}^\circ }}\]                      done clear
  B)
   \[{{150}^{{}^\circ }}\] done clear
  C)
   \[{{135}^{{}^\circ }}\]      done clear
  D)
   \[{{100}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer10)

  Two parallel lines are cut by a transversal then which of the following is true?

  (I) Pair of alternate interior angles are same.

  (II) Pair of corresponding angles are same.

  (III) Pair of interior angles on the same side of the transversal are complementary.

  A)
   I, II, III are true              done clear
  B)
   I, II are true done clear
  C)
   I, II are true                   done clear
  D)
   II, III are true done clear
  View Solution play_arrow

• question_answer11)
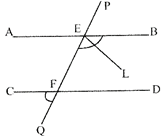
  AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of\[\angle \mathbf{FEB}\]. If \[\angle \mathbf{LEB}=\mathbf{5}{{\mathbf{5}}^{{}^\circ }}\]; then \[\angle \mathbf{DFQ}\] is equal to
  A)
   \[{{110}^{{}^\circ }}\]     done clear
  B)
   \[{{100}^{{}^\circ }}\] done clear
  C)
   \[{{115}^{{}^\circ }}\]                                   done clear
  D)
   \[{{105}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer12)
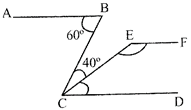
  AB and CD are two parallel lines. The points B and C are joined such that\[\angle \mathbf{ABC}=\mathbf{6}{{\mathbf{0}}^{{}^\circ }}\]. A line CE is drawn making angle of \[\mathbf{40}{}^\circ \] with the line CB, EF is drawn parallel to AB. As show in figure then \[\angle \mathbf{CEF}\] is equal to:
  A)
   \[{{160}^{{}^\circ }}\]       done clear
  B)
   \[{{150}^{{}^\circ }}\] done clear
  C)
   \[{{120}^{{}^\circ }}\]                                   done clear
  D)
   \[{{135}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer13)
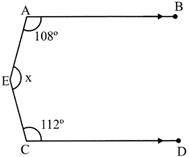
  In the given figure, \[\mathbf{AB}\parallel \mathbf{CD}\]. Then what is the value of x?
  A)
   \[{{140}^{{}^\circ }}\]           done clear
  B)
   \[{{45}^{{}^\circ }}\]            done clear
  C)
   \[{{120}^{{}^\circ }}\]                                   done clear
  D)
   \[{{75}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer14)
  In the given figure, if \[\mathbf{EC}\parallel \mathbf{AB},\]\[\angle \mathbf{ECD}=\mathbf{6}{{\mathbf{5}}^{{}^\circ }},\] \[\angle \mathbf{BDO}=\mathbf{2}{{\mathbf{5}}^{{}^\circ }}\], then \[\angle \mathbf{OBD}\] is to:
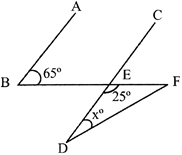
  A)
   \[{{40}^{{}^\circ }}\]       done clear
  B)
   \[{{65}^{{}^\circ }}\]             done clear
  C)
   \[{{115}^{{}^\circ }}\]                                   done clear
  D)
   \[{{70}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer15)
  Two parallel lines AB and CD are intersected by a transversal line EF at M and N respectively. The lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal. Then \[\angle \,\mathbf{MPN}\] is equal to:
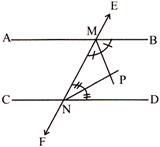
  A)
   \[{{90}^{{}^\circ }}\] done clear
  B)
   \[{{45}^{{}^\circ }}\] done clear
  C)
   \[{{135}^{{}^\circ }}\]                           done clear
  D)
   \[{{60}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer16)
  In the given figure, \[\mathbf{AB}\parallel \mathbf{GH}\parallel \mathbf{DE}\] and\[\mathbf{GF}\parallel \mathbf{BD}\parallel \mathbf{HI},\] \[\angle \mathbf{FGC}=\mathbf{10}{{\mathbf{0}}^{{}^\circ }}\]. Find the value of \[\angle \mathbf{CHL}\]
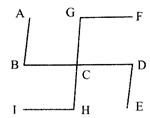
  A)
   \[{{80}^{{}^\circ }}\]                                    done clear
  B)
   \[{{120}^{{}^\circ }}\] done clear
  C)
   \[{{100}^{{}^\circ }}\]     done clear
  D)
   \[{{160}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer17)
  In the adjoining figure, \[\mathbf{AE}\parallel \mathbf{CD}\] and \[\mathbf{BC}\parallel \mathbf{ED}\], then y = ?
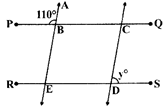
  A)
   \[{{60}^{{}^\circ }}\]                        done clear
  B)
   \[{{70}^{{}^\circ }}\] done clear
  C)
   \[{{90}^{{}^\circ }}\]                                    done clear
  D)
   \[{{75}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer18)
  In the adjoining figure, \[\mathbf{AB}\parallel \mathbf{CD}\] and PQ, QR intersect AB and CD both at E, F and G, H respectively. Given that \[\angle \mathbf{PEB}=\mathbf{7}{{\mathbf{0}}^{{}^\circ }},\]\[\angle \mathbf{QHD}=\mathbf{13}{{\mathbf{0}}^{{}^\circ }}\]and \[\angle \,\mathbf{PQR=x}{}^\circ ,\] find the value of \[{{\mathbf{x}}^{{}^\circ }}\].
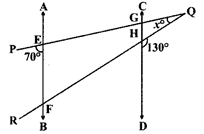
  A)
   \[{{40}^{{}^\circ }}\]                       done clear
  B)
   \[{{10}^{{}^\circ }}\] done clear
  C)
   \[{{20}^{{}^\circ }}\] done clear
  D)
   \[{{30}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer19)
  In the adjoining figure, A \[A\mathbf{B}\parallel \mathbf{DE}.\]\[\angle \mathbf{ABC}=\mathbf{5}{{\mathbf{7}}^{{}^\circ }}\]and\[\angle \mathbf{EDC}=\mathbf{3}{{\mathbf{3}}^{{}^\circ }}.\]Find\[\angle \mathbf{BCD}\]
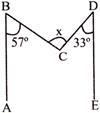
  A)
   \[{{90}^{{}^\circ }}\]   done clear
  B)
   \[{{50}^{{}^\circ }}\] done clear
  C)
   \[{{80}^{{}^\circ }}\]                                    done clear
  D)
   \[{{105}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer20)
  In the given figure, \[\mathbf{AB}\parallel \mathbf{DE}\]. Find \[\mathbf{a{}^\circ }+\mathbf{b{}^\circ }-\mathbf{c{}^\circ }.\]
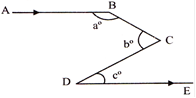
  A)
   \[{{160}^{{}^\circ }}\]                                   done clear
  B)
   \[{{120}^{{}^\circ }}\] done clear
  C)
   \[{{180}^{{}^\circ }}\]      done clear
  D)
   \[{{210}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer21)
  \[\mathbf{PQ}\parallel \mathbf{RS}\], as shown in the figure. Find the value of x.
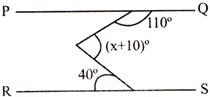
  A)
   \[{{90}^{{}^\circ }}\]                                    done clear
  B)
   \[{{80}^{{}^\circ }}\] done clear
  C)
   \[{{100}^{{}^\circ }}\]    done clear
  D)
   \[{{150}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer22)
  In the given figure, \[\mathbf{PQ}\parallel \mathbf{LM}\parallel \mathbf{RS}\]. What is the value of \[\angle \mathbf{RLM}\]?
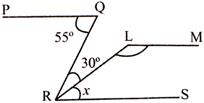
  A)
   \[{{20}^{{}^\circ }}\]                       done clear
  B)
   \[{{155}^{{}^\circ }}\] done clear
  C)
   \[{{30}^{{}^\circ }}\]                                    done clear
  D)
   \[{{45}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer23)
  In the given figure,\[\mathbf{AB}\parallel \mathbf{DC}\] and \[\mathbf{DE}\parallel \mathbf{BF}\]. What is the value of x?
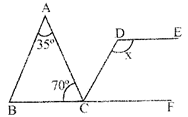
  A)
   \[{{140}^{{}^\circ }}\]                       done clear
  B)
   \[{{150}^{{}^\circ }}\] done clear
  C)
   \[{{105}^{{}^\circ }}\]    done clear
  D)
   \[{{120}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer24)
  In the given figure, \[\mathbf{AB}\parallel \mathbf{CD},\angle \mathbf{ABE}={{95}^{{}^\circ }}\], Find \[\angle \mathbf{CDE}\]:
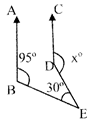
  A)
   \[{{120}^{{}^\circ }}\]                                   done clear
  B)
   \[{{110}^{{}^\circ }}\] done clear
  C)
   \[{{125}^{{}^\circ }}\]       done clear
  D)
   \[{{100}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer25)
  In the given figure, \[\mathbf{AB}\parallel \mathbf{CD}\], then \[{{\mathbf{x}}^{{}^\circ }}\]= ?
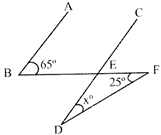
  A)
   \[{{40}^{{}^\circ }}\]   done clear
  B)
   \[{{70}^{{}^\circ }}\] done clear
  C)
   \[{{30}^{{}^\circ }}\]                           done clear
  D)
   \[{{90}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer26)
  In the given figure, \[\mathbf{XY}\parallel \mathbf{PQ}\], then the value of x is:
  A)
   \[{{75}^{{}^\circ }}\]                        done clear
  B)
   \[{{35}^{{}^\circ }}\] done clear
  C)
   \[{{65}^{{}^\circ }}\]     done clear
  D)
   \[{{45}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer27)
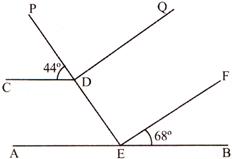
  In the given figure,\[\mathbf{AB}\parallel \mathbf{CD}\] and \[\mathbf{EF}\parallel \mathbf{DQ}\]. The value of \[\angle \mathbf{DEF}\] is:
  A)
   \[{{68}^{{}^\circ }}\]    done clear
  B)
   \[{{78}^{{}^\circ }}\] done clear
  C)
   \[{{44}^{{}^\circ }}\]                                    done clear
  D)
   \[{{100}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer28)
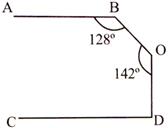
  \[\mathbf{AB}\parallel \mathbf{CD},\angle \mathbf{ABO}=\mathbf{12}{{\mathbf{8}}^{{}^\circ }},\angle \mathbf{BOD}=\mathbf{14}{{\mathbf{2}}^{{}^\circ }}\], Then, \[\angle \mathbf{ODC}\] = ?
  A)
   \[{{100}^{{}^\circ }}\]                      done clear
  B)
   \[{{80}^{{}^\circ }}\] done clear
  C)
   \[{{90}^{{}^\circ }}\]   done clear
  D)
   \[{{88}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer29)
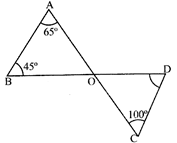
  In the given figure, \[\angle \mathbf{OAB}=\mathbf{6}{{\mathbf{5}}^{{}^\circ }},\]\[\angle \mathbf{OBA}=\mathbf{4}{{\mathbf{5}}^{{}^\circ }}\] and \[\angle \mathbf{OCD}=\mathbf{10}{{\mathbf{0}}^{{}^\circ }}\]. Then \[\angle \mathbf{ODC}\] =?
  A)
   \[{{20}^{{}^\circ }}\]                           done clear
  B)
   \[{{10}^{{}^\circ }}\] done clear
  C)
   \[{{30}^{{}^\circ }}\]                           done clear
  D)
   \[{{25}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer30)
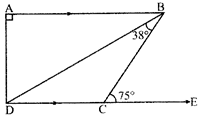
  In the given figure,\[\mathbf{AB}\parallel \mathbf{DC},\]\[\angle \mathbf{BAD}=\mathbf{9}{{\mathbf{0}}^{{}^\circ }},\]\[\angle \mathbf{CBD}=\mathbf{3}{{\mathbf{8}}^{{}^\circ }}\]and\[\angle \mathbf{BCE}=\mathbf{7}{{\mathbf{5}}^{{}^\circ }}\]. Then \[\angle \mathbf{ABD}\] = ?
  A)
   \[{{32}^{{}^\circ }}\]                                    done clear
  B)
   \[{{37}^{{}^\circ }}\] done clear
  C)
   \[{{34}^{{}^\circ }}\]                                    done clear
  D)
   \[{{35}^{{}^\circ }}\] done clear
  View Solution play_arrow