A) \[\frac{\pi }{2}\]
B) \[\frac{\pi }{4}\]
C) \[\frac{\pi }{3}\]
D) \[\pi \]
Correct Answer: C
Solution :
Required area \[=\int_{0}^{\sqrt{3}}{\frac{x}{\sqrt{3}}dx+\int_{\sqrt{3}}^{2}{\sqrt{4-{{x}^{2}}}dx}}\]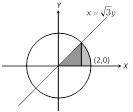 \[=\frac{1}{\sqrt{3}}\left[ \frac{{{x}^{2}}}{2} \right]_{0}^{\sqrt{3}}+\left[ \frac{x}{2}\sqrt{4-{{x}^{2}}}+\frac{4}{2}{{\sin }^{-1}}\frac{x}{2} \right]_{\sqrt{3}}^{2}\] \[=\frac{\sqrt{3}}{2}+\left[ \pi -\frac{\sqrt{3}}{2}-\frac{2\pi }{3} \right]=\frac{\pi }{3}\]. Trick : Area of sector made by an arc = \[\frac{{{\theta }^{c}}{{R}^{2}}}{2}\] \[=\frac{\pi }{6}.\frac{4}{2}=\frac{\pi }{3}\].
\[=\frac{1}{\sqrt{3}}\left[ \frac{{{x}^{2}}}{2} \right]_{0}^{\sqrt{3}}+\left[ \frac{x}{2}\sqrt{4-{{x}^{2}}}+\frac{4}{2}{{\sin }^{-1}}\frac{x}{2} \right]_{\sqrt{3}}^{2}\] \[=\frac{\sqrt{3}}{2}+\left[ \pi -\frac{\sqrt{3}}{2}-\frac{2\pi }{3} \right]=\frac{\pi }{3}\]. Trick : Area of sector made by an arc = \[\frac{{{\theta }^{c}}{{R}^{2}}}{2}\] \[=\frac{\pi }{6}.\frac{4}{2}=\frac{\pi }{3}\].
You need to login to perform this action.
You will be redirected in
3 sec
