A) \[{{a}^{2}}\]
B) \[2{{a}^{2}}\]
C) \[3{{a}^{2}}\]
D) \[4{{a}^{2}}\]
Correct Answer: B
Solution :
Given \[xy={{a}^{2}}\] or \[y=\frac{{{a}^{2}}}{x}\] .....(i) There are two points on the curve (a, a),(? a,? a)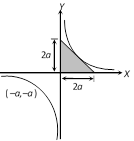 The equation of the line at \[(a,a)\]is, \[y-a={{\left( \frac{dy}{dx} \right)}_{(a,\,a)}}(x-a)\]\[={{\left( \frac{-{{a}^{2}}}{{{x}^{2}}} \right)}_{(a,\,a)}}(x-a)\] \[y-a=-(x-a)\] therefore, equation of the tangent at \[(a,a)\] is \[x+y=2\,a\].The interception of line \[x+y=2a\] with x-axis is 2a and with y-axis is 2a. \[\therefore \] Required area = \[\frac{1}{2}\times 2a\times 2a=2{{a}^{2}}\].
The equation of the line at \[(a,a)\]is, \[y-a={{\left( \frac{dy}{dx} \right)}_{(a,\,a)}}(x-a)\]\[={{\left( \frac{-{{a}^{2}}}{{{x}^{2}}} \right)}_{(a,\,a)}}(x-a)\] \[y-a=-(x-a)\] therefore, equation of the tangent at \[(a,a)\] is \[x+y=2\,a\].The interception of line \[x+y=2a\] with x-axis is 2a and with y-axis is 2a. \[\therefore \] Required area = \[\frac{1}{2}\times 2a\times 2a=2{{a}^{2}}\].
You need to login to perform this action.
You will be redirected in
3 sec
