A) \[\frac{1}{2}(9{{\sec }^{-1}}3-\sqrt{8})\]
B) \[9{{\sec }^{-1}}(3)-\sqrt{8}\]
C) \[\sqrt{8}-9{{\sec }^{-1}}(3)\]
D) None of these
Correct Answer: B
Solution :
Area of smaller part \[I=2\int_{1}^{3}{\sqrt{9-{{x}^{2}}}\,dx}\] \[=2.\frac{1}{2}\left[ x\sqrt{9-{{x}^{2}}}+9{{\sin }^{-1}}\frac{x}{3} \right]_{1}^{3}=\left[ 9\frac{\pi }{2}-\sqrt{8}-9{{\sin }^{-1}}\left( \frac{1}{3} \right) \right]\]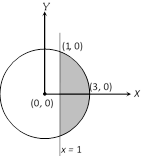 \[=\left[ 9\left( \frac{\pi }{2}-{{\sin }^{-1}}\left( \frac{1}{3} \right) \right)-\sqrt{8} \right]\]\[=\left[ 9{{\cos }^{-1}}\left( \frac{1}{3} \right)-\sqrt{8} \right]\] = \[[9{{\sec }^{-1}}(3)-\sqrt{8}]\].
\[=\left[ 9\left( \frac{\pi }{2}-{{\sin }^{-1}}\left( \frac{1}{3} \right) \right)-\sqrt{8} \right]\]\[=\left[ 9{{\cos }^{-1}}\left( \frac{1}{3} \right)-\sqrt{8} \right]\] = \[[9{{\sec }^{-1}}(3)-\sqrt{8}]\].
You need to login to perform this action.
You will be redirected in
3 sec
