A) \[\frac{{{\pi }^{2}}}{5}\]
B) \[\frac{{{\pi }^{2}}}{2}\]
C) \[\frac{{{\pi }^{2}}}{3}\]
D) \[\frac{\pi }{4}-\frac{1}{2}\]
Correct Answer: D
Solution :
\[{{x}^{2}}+{{y}^{2}}=1,x+y=1\]meet when \[{{x}^{2}}+{{(1-x)}^{2}}=1\Rightarrow {{x}^{2}}+1+{{x}^{2}}-2x=1\]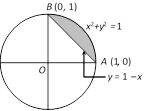 \[\Rightarrow 2{{x}^{2}}-2x=0\,\,\Rightarrow 2x(x-1)=0\] \[\Rightarrow x=0,\,x=1\] Þ \[y=1,\,y=0\], i.e., \[A\,(1,0);\,\,B\,(0,1)\] Required area \[=\int_{0}^{1}{[\sqrt{1-{{x}^{2}}}-(1-x)]}\]dx \[=\left[ \frac{x\sqrt{1-{{x}^{2}}}}{2}+\frac{1}{2}{{\sin }^{-1}}x-x+\frac{{{x}^{2}}}{2} \right]_{0}^{1}\] \[=\frac{1}{2}.\frac{\pi }{2}-1+\frac{1}{2}=\frac{\pi }{4}-\frac{1}{2}\].
\[\Rightarrow 2{{x}^{2}}-2x=0\,\,\Rightarrow 2x(x-1)=0\] \[\Rightarrow x=0,\,x=1\] Þ \[y=1,\,y=0\], i.e., \[A\,(1,0);\,\,B\,(0,1)\] Required area \[=\int_{0}^{1}{[\sqrt{1-{{x}^{2}}}-(1-x)]}\]dx \[=\left[ \frac{x\sqrt{1-{{x}^{2}}}}{2}+\frac{1}{2}{{\sin }^{-1}}x-x+\frac{{{x}^{2}}}{2} \right]_{0}^{1}\] \[=\frac{1}{2}.\frac{\pi }{2}-1+\frac{1}{2}=\frac{\pi }{4}-\frac{1}{2}\].
You need to login to perform this action.
You will be redirected in
3 sec
