A) \[9\pi /5\]
B) \[4\pi /3\]
C) \[8\pi /3\]
D) \[7\pi /5\]
Correct Answer: B
Solution :
Volume of the solid formed by rotating the area enclosed between the curve \[y={{x}^{2}}\] and line \[y=1\] will be \[\int_{0}^{1}{2\pi \,xdy}\]= \[2\int_{0}^{1}{\pi \sqrt{y}dy}\]= \[\frac{4\pi }{3}[{{y}^{3/2}}]_{0}^{1}=\frac{4\pi }{3}\].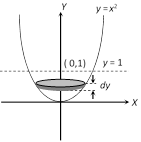
You need to login to perform this action.
You will be redirected in
3 sec
