A) \[\frac{{{a}^{2}}}{3}\] sq. unit
B) \[\frac{1}{3{{a}^{2}}}\] sq. unit
C) \[\frac{1}{3a}\] sq. unit
D) \[\frac{2}{3a}\] sq. unit
Correct Answer: C
Solution :
The points of intersection of the parabola \[{{y}^{2}}=4ax\]and the chord\[y=2ax\]is obtained by solving these equations simultaneously. \[{{y}^{2}}=4ax,y=2ax\Rightarrow {{(2ax)}^{2}}=4ax\] Þ \[x[4{{a}^{2}}x-4a]=0\]\[\Rightarrow 4ax[ax-1]=0\] Þ \[x=0\]or \[x=\frac{1}{a}\]Also \[x=0\Rightarrow y=0\]and \[x=\frac{1}{a}\] Þ\[y=\pm 2\]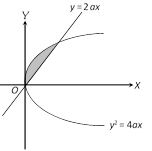 Hence the required points are (0,0) and \[\left[ \frac{1}{a},2 \right]\]. Now required area\[=\int_{0}^{1/a}{[\sqrt{4ax}-2ax}]dx=\frac{1}{3a}sq\]. unit.
Hence the required points are (0,0) and \[\left[ \frac{1}{a},2 \right]\]. Now required area\[=\int_{0}^{1/a}{[\sqrt{4ax}-2ax}]dx=\frac{1}{3a}sq\]. unit.
You need to login to perform this action.
You will be redirected in
3 sec
