question_answer

The parabolas \[{{y}^{2}}=4x\] and \[{{x}^{2}}=4y\] divide the square region bounded by the lines \[x=4\], \[y=4\]and the coordinate axes. If \[{{S}_{1}},{{S}_{2}},{{S}_{3}}\] are respectively the areas of these parts numbered from top to bottom, then \[{{S}_{1}}:{{S}_{2}}:{{S}_{3}}\] is                                                            [AIEEE 2005]

A)            \[2:1:2\]                                 

B)            \[1:1:1\]                                 

C)            \[1:2:1\]                                 

D)            \[1:2:3\]

Correct Answer: B

Solution :

           \[{{y}^{2}}=4x\] and \[{{x}^{2}}=4y\] are symmetric about line \[y=x\]                    Þ Area bounded between \[{{y}^{2}}=4x\] and \[y=x\] is \[\int_{0}^{4}{(2\sqrt{x}-x)dx=\frac{8}{3}}\]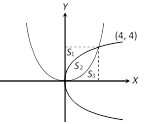                                       Þ  \[{{A}_{s}}_{_{2}}=\frac{16}{3}\] and \[{{A}_{{{s}_{1}}}}={{A}_{{{S}_{3}}}}=\frac{16}{3}\]                    Þ \[{{A}_{{{S}_{1}}}}:{{A}_{{{S}_{2}}}}:{{A}_{{{S}_{2}}}}::1:1:1\].