A) 6 sq. unit
B) 5/6 sq. unit
C) 1/6 sq. unit
D) None of these
Correct Answer: C
Solution :
\[\frac{dy}{dx}=2x+1\] Þ \[y={{x}^{2}}+x+c\] Þ \[y={{x}^{2}}+x\], [\[\because \] c = 0 by putting x = 1, y = 2) Þ \[{{\left( x+\frac{1}{2} \right)}^{2}}=y+\frac{1}{4}\], which is a equation of parabola, whose vertices is, \[V\left( \frac{-1}{2},\,\frac{-1}{4} \right)\]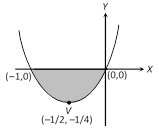 \[\therefore \] Required area \[=\left. \left| \int_{-1}^{0}{({{x}^{2}}+x)\ dx} \right. \right|\] \[=\left( \frac{{{x}^{3}}}{3}+\frac{{{x}^{2}}}{2} \right)_{-1}^{0}\] \[\left. =\left| \frac{-1}{3}+\frac{1}{2} \right. \right|=\frac{1}{6}\] sq. unit.
\[\therefore \] Required area \[=\left. \left| \int_{-1}^{0}{({{x}^{2}}+x)\ dx} \right. \right|\] \[=\left( \frac{{{x}^{3}}}{3}+\frac{{{x}^{2}}}{2} \right)_{-1}^{0}\] \[\left. =\left| \frac{-1}{3}+\frac{1}{2} \right. \right|=\frac{1}{6}\] sq. unit.
You need to login to perform this action.
You will be redirected in
3 sec
