question_answer

ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then

A)  area \[\left( \Delta BCP \right)\] = area \[\left( \Delta DPQ \right)\]

B)  area \[\left( \Delta BCP \right)\] > area \[\left( \Delta DPQ \right)\]

C)  area \[\left( \Delta BCP \right)\] < area \[\left( \Delta DPQ \right)\]

D)  area \[\left( \Delta BCP \right)\] + area \[\left( \Delta DPQ \right)\] = area \[(\Delta \,BCD)\]

Correct Answer: A

Solution :

(a): Join \[AC\And DQ\therefore \Delta APC\] and \[\Delta BCP\] lie on the same base PC and between the same parallels AB and PC \[\therefore ar\left( \Delta APC \right)=ar\left( \Delta BCP \right)\]             ....(i) Now, \[AD\parallel CQ\] and \[AD=CQ\] \[\therefore \] \[\Delta DQC\] is a parallelogram, Again \[\Delta ADC\] and \[\Delta DAQ\] are on the same base AD and between same parallels AD and CQ.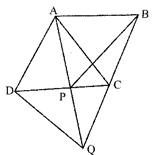             \[\therefore ar\left( \Delta ADC \right)=ar\left( \Delta ADQ \right)\] Subtracting ar (DAP) from both sides, we get ar\[\left( \Delta APC \right)\]=ar\[\left( \Delta DPQ \right)\]       .....(ii) From (i) and (ii), we get ar \[\left( \Delta BCP \right)\] = ar\[\left( \Delta DPQ \right)\]