| Case Study : Q. 1 to 5 |
| Amit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is \[\text{95 sq}.\text{ m}\]. |
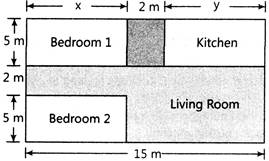 |
| Based on the above information, give the answer of the following questions: |
A) \[2x+y=19,\,\,x+y=13\]
B) \[x+2y=19,\,\,x+y=18\]
C) \[x+y=19,\,\,x+2y=13\]
D) \[x+3y=19,2\,x+y=15\]
Correct Answer: A
Solution :
| Given that, length of bedroom \[=x\,m\] |
| And breadth of bedroom \[=5\,m\] |
| \[\therefore \] Area of a bedroom \[=5x\,\,sq.\,m\] |
| So, area of two bedrooms \[=2\times 5x=10x\,sq.\,m\] |
| Also, length of kitchen \[=y\,m\] |
| and breadth of kitchen \[=\,5\,\,m\] |
| \[\therefore \] Area of the kitchen \[=5y\,\,sq.\,m\] |
| According to question, |
| Areas of two bedrooms and kitchen together \[=95\,\,sq.\,m\] |
| \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,10x+5y=95\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,2x+y=19\] ..(1) |
| (divide both sides by 5) |
| According to figure, |
| Length of a bedroom + length of bathroom + length of the kitchen = Length of the layout of the house |
| \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,\,\,x+2+y=15\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,x+y=13\] ..(2) |
| Hence, eqs. (1) and (2) represent the pair of linear equations in two variables. |
| So, option [a] is correct. |
You need to login to perform this action.
You will be redirected in
3 sec
