| Case Study : Q. 11 to 15 | |
| Applications of parabolas - highway overpasses/ underpasses. A highway underpass is parabolic in shape. | |
 | |
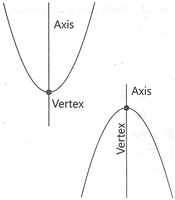
| Parabola: A parabola is the graph that results from \[p(x)=a{{x}^{2}}+bx+c\] Parabolas are symmetric about a vertical line known as the axis of symmetry. | |
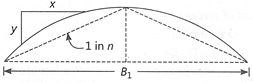 | |
| Parabolic chamber \[y=2{{x}^{2}}/nw\] | |
| The axis of symmetry runs through the maximum or minimum point of the parabola which is called the vertex. | |
 | |
| Based on the above information, answer the following questions. | |
| If the highway overpass is represented by \[{{x}^{2}}-2x-8\]. | |
| Then its zeroes are: | |
A) \[(2,-4)\]
B) \[(4,-2)\]
C) \[(-2,-2)\]
D) \[(-4,-4)\]
Correct Answer: B
Solution :
| \[{{x}^{2}}-2x-8\] |
| [TRICK \[8=2\times 4=8\times 1\] \[\therefore \] Here, we will take 2 and 4 as a factors of 8. So, middle term becomes, \[-2=-4+2\] ] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}^{2}}-4x+2x-8\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,x(x-4)\,\,+2\,(x-4)\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,(x-4)\,\,(x+2)\] |
| For zeroes. |
| \[x-4=0\] or \[x+2=0\] |
| \[x=4\] and \[-2\] |
| So, option [b] is correct. |
You need to login to perform this action.
You will be redirected in
3 sec
