question_answer

A pair of straight lines drawn through the origin form with the line \[2x+3y=6\]an isosceles right angled triangle, then the lines and the area of the triangle thus formed is                                                    [Roorkee 1993]

A)            \[x-5y=0\]\[5x+y=0\]\[\Delta =\frac{36}{13}\]                           

B)            \[3x-y=0\]\[x+3y=0\]\[\Delta =\frac{12}{17}\]

C)            \[5x-y=0\]\[x+5y=0\]\[\Delta =\frac{13}{5}\]                             

D)            None of these

Correct Answer: A

Solution :

           \[y=mx\]. It makes an angle of \[\pm {{45}^{o}}\] with \[2x+3y=6\].                    \ \[\tan (\pm {{45}^{o}})=\frac{m-(-2/3)}{1+m(-2/3)}=\pm 1\]                    or \[3m+2=\pm (3-2m)\]\[\Rightarrow m=\frac{1}{5},-5\]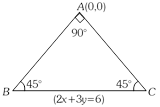 Hence sides are                    \[x-5y=0,\]                    \[5x+y=0\]                    and \[2x+3y=6\].                    Solving in pairs, vertices are \[(0,\,0)\],                    \[\left( \frac{6}{13},\frac{30}{13} \right)\,,\left( \frac{30}{13},-\frac{6}{13} \right)\].                    \[\Delta =\left| \frac{1}{2}({{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}}) \right|=\frac{1}{2}\times \frac{936}{169}=\frac{36}{13}\].