question_answer

The locus of the middle point of the intercept of the tangents drawn from an external point to the ellipse \[{{x}^{2}}+2{{y}^{2}}=2\] between the co-ordinates axes, is                                                      [IIT Screening 2004]

A)            \[\frac{1}{{{x}^{2}}}+\frac{1}{2{{y}^{2}}}=1\]                              

B)            \[\frac{1}{4{{x}^{2}}}+\frac{1}{2{{y}^{2}}}=1\]

C)            \[\frac{1}{2{{x}^{2}}}+\frac{1}{4{{y}^{2}}}=1\]                            

D)            \[\frac{1}{2{{x}^{2}}}+\frac{1}{{{y}^{2}}}=1\]

Correct Answer: C

Solution :

           Let the point of contact be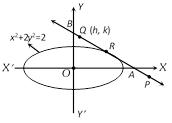            \[R\equiv (\sqrt{2}\cos \theta ,\,\sin \theta )\]            Equation of tangent AB is            \[\frac{x}{\sqrt{2}}\cos \theta +y\sin \theta =1\]            \[\Rightarrow \]\[A\equiv (\sqrt{2}\sec \theta ,\,0);\,B\equiv (0,\,\text{cosec }\theta )\]            Let the middle point Q of AB be \[(h,\,k)\]            \[\Rightarrow \] \[h=\frac{\sec \theta }{\sqrt{2}},\,k=\frac{\text{cosec }\theta }{2}\Rightarrow \cos \theta =\frac{1}{h\sqrt{2}},\,\sin \theta =\frac{1}{2k}\]            \[\Rightarrow \] \[\frac{1}{2{{h}^{2}}}+\frac{1}{4{{k}^{2}}}=1\], \Required locus is \[\frac{1}{2{{x}^{2}}}+\frac{1}{4{{y}^{2}}}=1\].            Trick :  The locus of mid-points of the portion of tangents to the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] intercepted between axes is \[{{a}^{2}}{{y}^{2}}+{{b}^{2}}{{x}^{2}}=4{{x}^{2}}{{y}^{2}}\]            i.e., \[\frac{{{a}^{2}}}{4{{x}^{2}}}+\frac{{{b}^{2}}}{4{{y}^{2}}}=1\] or \[\frac{1}{2{{x}^{2}}}+\frac{1}{4{{y}^{2}}}=1\].