A) \[1<e<2/\sqrt{3}\]
B) \[e=2/\sqrt{3}\]
C) \[e=\sqrt{3}/2\]
D) \[e>2/\sqrt{3}\]
Correct Answer: D
Solution :
Let P \[(a\sec \theta ,\,b\tan \theta );\,Q(a\sec \theta ,\,-b\tan \theta )\] be end points of double ordinates and \[C(0,\,0)\], is the centre of the hyperbola. Now \[PQ=2b\,\tan \theta \]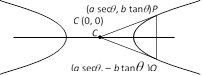 \[CQ=CP=\sqrt{{{a}^{2}}{{\sec }^{2}}\theta +{{b}^{2}}{{\tan }^{2}}\theta }\] Since \[CQ=CP=PQ\], \[\therefore \,4{{b}^{2}}{{\tan }^{2}}\theta ={{a}^{2}}{{\sec }^{2}}\theta +{{b}^{2}}{{\tan }^{2}}\theta \] Þ \[3{{b}^{2}}{{\tan }^{2}}\theta ={{a}^{2}}{{\sec }^{2}}\theta \] Þ \[3{{b}^{2}}{{\sin }^{2}}\theta ={{a}^{2}}\] Þ \[3{{a}^{2}}({{e}^{2}}-1){{\sin }^{2}}\theta ={{a}^{2}}\]Þ \[3({{e}^{2}}-1){{\sin }^{2}}\theta =1\] Þ \[\frac{1}{3({{e}^{2}}-1)}={{\sin }^{2}}\theta <1\], \[(\because \,{{\sin }^{2}}\theta <1)\] \[\Rightarrow \] \[\frac{1}{{{e}^{2}}-1}<3\]\[\Rightarrow \,\,{{e}^{2}}-1>\frac{1}{3}\]\[\Rightarrow \,\,{{e}^{2}}>\frac{4}{3}\]\[\Rightarrow \,e>\frac{2}{\sqrt{3}}\].
\[CQ=CP=\sqrt{{{a}^{2}}{{\sec }^{2}}\theta +{{b}^{2}}{{\tan }^{2}}\theta }\] Since \[CQ=CP=PQ\], \[\therefore \,4{{b}^{2}}{{\tan }^{2}}\theta ={{a}^{2}}{{\sec }^{2}}\theta +{{b}^{2}}{{\tan }^{2}}\theta \] Þ \[3{{b}^{2}}{{\tan }^{2}}\theta ={{a}^{2}}{{\sec }^{2}}\theta \] Þ \[3{{b}^{2}}{{\sin }^{2}}\theta ={{a}^{2}}\] Þ \[3{{a}^{2}}({{e}^{2}}-1){{\sin }^{2}}\theta ={{a}^{2}}\]Þ \[3({{e}^{2}}-1){{\sin }^{2}}\theta =1\] Þ \[\frac{1}{3({{e}^{2}}-1)}={{\sin }^{2}}\theta <1\], \[(\because \,{{\sin }^{2}}\theta <1)\] \[\Rightarrow \] \[\frac{1}{{{e}^{2}}-1}<3\]\[\Rightarrow \,\,{{e}^{2}}-1>\frac{1}{3}\]\[\Rightarrow \,\,{{e}^{2}}>\frac{4}{3}\]\[\Rightarrow \,e>\frac{2}{\sqrt{3}}\].
You need to login to perform this action.
You will be redirected in
3 sec
