question_answer

An ellipse has eccentricity \[\frac{1}{2}\] and one focus at the point\[P\left( \frac{1}{2},\ 1 \right)\]. Its one directrix is the common tangent nearer to the point P, to the circle \[{{x}^{2}}+{{y}^{2}}=1\] and the hyperbola\[{{x}^{2}}-{{y}^{2}}=1\]. The equation of the ellipse in the standard form, is       [IIT 1996]

A)            \[\frac{{{(x-1/3)}^{2}}}{1/9}+\frac{{{(y-1)}^{2}}}{1/12}=1\]

B)            \[\frac{{{(x-1/3)}^{2}}}{1/9}+\frac{{{(y+1)}^{2}}}{1/12}=1\]

C)            \[\frac{{{(x-1/3)}^{2}}}{1/9}-\frac{{{(y-1)}^{2}}}{1/12}=1\]

D)            \[\frac{{{(x-1/3)}^{2}}}{1/9}-\frac{{{(y+1)}^{2}}}{1/12}=1\]

Correct Answer: A

Solution :

           There are two common tangents to the circle \[{{x}^{2}}+{{y}^{2}}=1\] and the hyperbola \[{{x}^{2}}-{{y}^{2}}=1.\] These are \[x=1\] and \[x=-1\]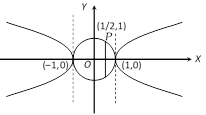                   Out of these, \[x=1\] is nearer to the point \[P(1/2,1)\].                   Thus a directrix of the required ellipse is \[x=1.\]            If \[Q(x,y)\] is any point on the ellipse, then its distance from the focus is \[QP=\sqrt{{{\left( x-\frac{1}{2} \right)}^{2}}+{{(y-1)}^{2}}}\] and its distance from the directrix \[x=1\]is \[|x-1|\].            By definition of ellipse, \[QP=e|x-1|\]            \[\Rightarrow \sqrt{{{\left( x-\frac{1}{2} \right)}^{2}}+{{(y-1)}^{2}}}=\frac{1}{2}|x-1|\]                    Þ\[3{{x}^{2}}-2x+4{{y}^{2}}-8y+4=0\]or\[\frac{{{\left( x-\frac{1}{3} \right)}^{2}}}{1/9}+\frac{{{(y-1)}^{2}}}{1/12}=1\].