A) \[23x+14y-40=0\]
B) \[14x-23y+40=0\]
C) \[{{\tan }^{-1}}(2)\]
D) \[14x+23y-40=0\]
Correct Answer: D
Solution :
Let the equation of perpendicular bisector FN of AB is \[x-y+5=0\] ......(i)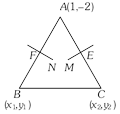 The middle point F of AB is \[\left( \frac{{{x}_{1}}+1}{2},\frac{{{y}_{1}}-2}{2} \right)\]lies on line (i). Therefore \[{{x}_{1}}-{{y}_{1}}=-13\] ?..(ii) Also AB is perpendicular to FN. So the product of their slopes is ?1. i.e. \[\frac{{{y}_{1}}+2}{{{x}_{1}}-1}\times 1=-1\]or \[{{x}_{1}}+{{y}_{1}}=-1\] ??(iii) On solving (ii) and (iii), we get \[B(-7,6)\]. Similarly \[C\text{ }\left( \frac{11}{5},\frac{2}{5} \right)\]. Hence the equation of BC is \[14x+23y-40=0\].
The middle point F of AB is \[\left( \frac{{{x}_{1}}+1}{2},\frac{{{y}_{1}}-2}{2} \right)\]lies on line (i). Therefore \[{{x}_{1}}-{{y}_{1}}=-13\] ?..(ii) Also AB is perpendicular to FN. So the product of their slopes is ?1. i.e. \[\frac{{{y}_{1}}+2}{{{x}_{1}}-1}\times 1=-1\]or \[{{x}_{1}}+{{y}_{1}}=-1\] ??(iii) On solving (ii) and (iii), we get \[B(-7,6)\]. Similarly \[C\text{ }\left( \frac{11}{5},\frac{2}{5} \right)\]. Hence the equation of BC is \[14x+23y-40=0\].
You need to login to perform this action.
You will be redirected in
3 sec
