-
question_answer1)
If \[A=\{1,2,3,4,5\}\], then the number of proper subsets of A is
A)
31 done
clear
B)
38 done
clear
C)
48 done
clear
D)
54 done
clear
View Solution play_arrow
-
question_answer2)
Which of the following is true?
A)
\[a\in \{\{a\},b\}\] done
clear
B)
\[\{b,c\}\subset \{a,\{b,c\}\}\] done
clear
C)
\[\{a,b\}\subset \{a,\{b,c\}\}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer3)
Let S be a set of all distinct numbers of the form \[\frac{P}{Q}\], where \[p,q\in \{1,2,3,4,5,6\}.\] What is the cardinality of the set S?
A)
21 done
clear
B)
23 done
clear
C)
32 done
clear
D)
36 done
clear
View Solution play_arrow
-
question_answer4)
Which of the following is a singleton set?
A)
\[\{x:\left| x \right|=5,x\in N\}\] done
clear
B)
\[\{x:\left| x \right|=6,x\in Z\}\] done
clear
C)
\[\{x:{{x}^{2}}+2x+1=0,x\in N\}\] done
clear
D)
\[\{x:{{x}^{2}}=7,x\in N\}\] done
clear
View Solution play_arrow
-
question_answer5)
Let\[A=\{x|x\le 9,x\in N\}\]. Let \[B=\{a,b,c\}\] be the subset of A where \[\left( a+b+c \right)\] is a multiple of 3. What is the largest possible number of subsets like B?
A)
12 done
clear
B)
21 done
clear
C)
27 done
clear
D)
30 done
clear
View Solution play_arrow
-
question_answer6)
Two finite sets have m and n elements, the total number of subsets of the first set is 56 more than the total number of subsets of the second set. Then:
A)
\[m=3,n=6\] done
clear
B)
\[m=6,n=3\] done
clear
C)
\[m=5,n=6\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer7)
If P denotes the power set of A and A is the void set, then what is number of elements in \[P\{P\{P\{P(A)\}\}\}\]?
A)
0 done
clear
B)
1 done
clear
C)
4 done
clear
D)
16 done
clear
View Solution play_arrow
-
question_answer8)
Which of the following sets is a finite set?
A)
\[A=\{x:x\in Z\,\,and\,\,{{x}^{2}}-5x+6=0\}\] done
clear
B)
\[B=\{x:x\in Z\,\,and\,\,{{x}^{2}}\,is\,even\}\] done
clear
C)
\[D=\{x:x\in Z\,\,and\,\,x>-10\}\] done
clear
D)
All of these done
clear
View Solution play_arrow
-
question_answer9)
Let S = the set of all triangles, P= the set of all isosceles triangles, Q= the set of all equilateral triangles, R= the set of all right - angled triangles. What do the sets \[P\cap Q\] and \[R-P\] represents respectively?
A)
The set of isosceles triangles; the set of non-isosceles right angled triangles done
clear
B)
The set of isosceles triangles; the set of right angled triangles done
clear
C)
The set of equilateral triangles; the set of right angled triangles done
clear
D)
The set of isosceles triangles; the set of equilateral triangles done
clear
View Solution play_arrow
-
question_answer10)
If A, B, C are there sets, then what is \[A-(B-C)\]equal to?
A)
\[A-(B\cap C)\] done
clear
B)
\[(A-B)\cup C\] done
clear
C)
\[(A-B)\cup (A\cap C)\] done
clear
D)
\[(A-B)\cup (A-C)\] done
clear
View Solution play_arrow
-
question_answer11)
If A and B are two sets, then \[(A-B)\cup (B-A)\]\[\cup (A\cap B)\] is equal to
A)
Only A done
clear
B)
\[A\cup B\] done
clear
C)
\[(A\cup B')\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer12)
Each student in a class of 40, studies at least one of the subjects English, Mathematics and Economics. 16 study English, 22 Economics and 26 Mathematics, 5 study English and? Economics, 14 Mathematics and Economics and 2 study all the three subjects. The number of students who study English and Mathematics but not Economics is
A)
7 done
clear
B)
5 done
clear
C)
10 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer13)
If A and B are subsets of a set X, then what is \[\{A\cap (X-B)\}\cup B\] equal to?
A)
\[A\cup B\] done
clear
B)
\[A\cap B\] done
clear
C)
A done
clear
D)
B done
clear
View Solution play_arrow
-
question_answer14)
A survey of 500 television viewers produced the following information, 285 watch football, 195 watch hockey, 115 watch basket-ball, 45 watch football and basketball, 70 watch football and hockey, 50 watch hockey and basketball, 50 do not watch any of the three games. The number of viewers, who watch exactly one of the three games are
A)
325 done
clear
B)
310 done
clear
C)
405 done
clear
D)
372 done
clear
View Solution play_arrow
-
question_answer15)
If \[A=\{4n+2|n\] is a natural number} and \[B=\{3n|n\] is a natural number,}, then what is \[(A\cap B)\] equal to?
A)
\[\{12{{n}^{2}}+6n|n\] is a natural number} done
clear
B)
\[\{24n-12|n\] is a natural number} done
clear
C)
\[\{60n+30|n\] is a natural number} done
clear
D)
\[\{12n-6|n\] is a natural number} done
clear
View Solution play_arrow
-
question_answer16)
A dinner party is to be fixed for a group of 100 persons. In this party, 50 persons do not prefer fish, 60 prefer chicken and 10 do not prefer either chicken of fish. The number of persons who prefer both fish and chicken is.
A)
20 done
clear
B)
22 done
clear
C)
25 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer17)
Which is the simplified representation of \[(A'\cap B'\cap C)\cup (B\cap C)\cup (A\cap C)\] where A, B, C are subsets of set X?
A)
A done
clear
B)
B done
clear
C)
C done
clear
D)
\[X\cap (A\cup B\cup C)\] done
clear
View Solution play_arrow
-
question_answer18)
Which one of the following is correct?
A)
\[A\cup (B-C)=A\cap (B\cap C')\] done
clear
B)
\[A-(B\cup C)=(A\cap B')\cap C'\] done
clear
C)
\[A-(B\cap C)=(A\cap B')\cap C\] done
clear
D)
\[A\cap (B-C)=(A\cap B)\cap C\] done
clear
View Solution play_arrow
-
question_answer19)
If F (n) denotes the set of all divisors of n except 1. What is the least value of y satisfying \[[F(20)\cap F(16)]\subseteq F(y)?\]
A)
1 done
clear
B)
2 done
clear
C)
4 done
clear
D)
8 done
clear
View Solution play_arrow
-
question_answer20)
If \[\mu \] is the universal set and P is a subset of \[\mu \], then what is \[P\cap (P-\mu )\cup (\mu -P)\}\] equal to?
A)
\[\phi \] done
clear
B)
P? done
clear
C)
m done
clear
D)
P done
clear
View Solution play_arrow
-
question_answer21)
Consider the following statements: For non-empty sets. A, B and C
| 1. \[A-(B-C)=(A-B)\cup C\] |
| 2. \[A-(B\cup C)=(A-B)-C\] |
Which of the statements given above is/are correct?
A)
1 only done
clear
B)
2 only done
clear
C)
Both 1 and 2 done
clear
D)
neither 1 nor 2 done
clear
View Solution play_arrow
-
question_answer22)
In a group of 500 students, there are 475 students who can speak Hindi and 200 can speak Bengali. What is the number of students who can speak Hindi only?
A)
275 done
clear
B)
300 done
clear
C)
325 done
clear
D)
350 done
clear
View Solution play_arrow
-
question_answer23)
Consider the following:
| 1. \[A\cup (B\cap C)=(A\cap B)\cup (A\cap C)\] |
| 2. \[A\cap (B\cup C)=(A\cup B)\cap (A\cup C)\] |
Which of the above is/are correct?
A)
1 only done
clear
B)
2 only done
clear
C)
Both 1 and 2 done
clear
D)
Neither 1 nor 2 done
clear
View Solution play_arrow
-
question_answer24)
In a city 20 percent of the population travels by car, 50 percent travels by bus and 10 percent travels by both car and bus. Then person travelling by car or bus is
A)
80 percent done
clear
B)
40 percent done
clear
C)
60 percent done
clear
D)
70 percent done
clear
View Solution play_arrow
-
question_answer25)
In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple as well as orange juice. Then, which of the following is/are true?
| I. 150 students were taking at least one juice. |
| II. 225 students were taking neither apple juice nor orange juice. |
A)
Only I is true done
clear
B)
Only II is true done
clear
C)
Both I and II are true done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer26)
If A, B and C are three finite sets, then what is \[\left[ (A\cup B)\cap C \right]'\] equal to?
A)
\[A'\cup B'\cap C'\] done
clear
B)
\[A'\cap B'\cap C'\] done
clear
C)
\[A'\cap B'\cup C'\] done
clear
D)
\[A\cap B\cap C\] done
clear
View Solution play_arrow
-
question_answer27)
A market research group conducted a survey of 2000 consumers and reported that 1720 consumers like product \[{{P}_{1}}\] and 1450 consumers like product \[{{P}_{2}}.\] What is the least number that must have liked both the products?
A)
1150 done
clear
B)
2000 done
clear
C)
1170 done
clear
D)
2500 done
clear
View Solution play_arrow
-
question_answer28)
If n = 115, n = 326, n(A - B) = 47, then what in \[n(A\cup B)\] equal to?
A)
373 done
clear
B)
165 done
clear
C)
370 done
clear
D)
394 done
clear
View Solution play_arrow
-
question_answer29)
If X and Y are two sets such that \[(X\cup Y)\] has 60 elements, X has 38 elements and Y has 42 elements, how many elements does \[(X\cap Y)\]have?
A)
11 done
clear
B)
20 done
clear
C)
13 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer30)
Let A, B, C be finite sets. Suppose that \[n(A)=10,\]\[n(B)=15,\] \[n(C)=20,\] \[n(A\cap B)=8\] and \[n(B\cap C)=9.\] Then the possible value of \[n(A\cup B\cup C)\] is
A)
26 done
clear
B)
27 done
clear
C)
28 done
clear
D)
Any of the three values 26, 27, 28 is possible done
clear
View Solution play_arrow
-
question_answer31)
A survey shows that 61%, 46% and 29% of the people watched ?3 idiots??, ?Raajneeti? and ?Avatar? respectively. 25% people watched exactly two of the three movies and 3% watches none. What percentage of people watched all the three movies?
A)
39% done
clear
B)
11% done
clear
C)
14% done
clear
D)
7% done
clear
View Solution play_arrow
-
question_answer32)
In a class of 80 students numbered a to 80, all odd numbered students opt if Cricket, students whose numbers are divisible by 5 opt for football and those whose numbers are divisible by 7 opt for Hockey. The number of students who do not opt any of the three games, is
A)
13 done
clear
B)
24 done
clear
C)
28 done
clear
D)
52 done
clear
View Solution play_arrow
-
question_answer33)
20 teachers of a school either teach mathematics or physics. 12 of them teach mathematics while 4 teach both the subjects. Then the number of teachers teaching physics only is
A)
12 done
clear
B)
8 done
clear
C)
16 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer34)
In a B School there are 15 teachers who teach marketing or finance. Of these, 8 teach finance. How many teach marketing but not finance?
A)
15 done
clear
B)
20 done
clear
C)
11 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer35)
The cardinality of the set \[P\left\{ P\left[ P(\phi ) \right] \right\}\] is
A)
0 done
clear
B)
1 done
clear
C)
2 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer36)
The number of elements in the set \[\{(a,b):2{{a}^{2}}+3{{b}^{2}}=35,a,b\in Z\}\], where Z is the set of all integers, is
A)
2 done
clear
B)
4 done
clear
C)
8 done
clear
D)
12 done
clear
View Solution play_arrow
-
question_answer37)
Which of the following is/are true?
| I. If A is a subset of the universal set U then its complement A? is also a subset of U. |
| II. If \[U=\{1,2,3,....,10\}\] and \[A=\{1,3,5,7,9\}\]then \[{{(A')}^{'}}=A.\] |
A)
Only I is true done
clear
B)
Only II is true done
clear
C)
Both I and II are true done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer38)
For a set A, consider the following statements:
| 1. \[A\cup P(A)=P(A)\] |
| 2. \[\{A\}\cap P(A)=A\] |
| 3. \[P(A)-\{A\}=P(A)\] |
where P denotes power set. Which of the statements given above is/are correct?
A)
1 only done
clear
B)
2 only done
clear
C)
3 only done
clear
D)
1, 2 and 3 done
clear
View Solution play_arrow
-
question_answer39)
If A and B are two disjoint sets, then which one of the following is correct?
A)
\[A-B=A-(A\cap B)\] done
clear
B)
\[B-A'=A\cap B\] done
clear
C)
\[A\cap B=(A-B)\cap B\] done
clear
D)
All of these done
clear
View Solution play_arrow
-
question_answer40)
Let n denote the set of natural numbers and \[A=\{{{n}^{2}}:n\in N\}\] and \[B=\{{{n}^{3}}:n\in N\},\] which one of the following is incorrect?
A)
\[A\cup B=N\] done
clear
B)
The complement of \[(A\cup B)\] is an infinite set done
clear
C)
\[A\cap B\] Must be a finite set done
clear
D)
\[A\cap B\] Must be proper subset of \[\{{{m}^{6}}:m\in N\}\] done
clear
View Solution play_arrow
-
question_answer41)
If the cardinality of a set A is 4 and that of a set B in 3, then what is the cardinality of the set A \[\Delta \] B?
A)
1 done
clear
B)
5 done
clear
C)
7 done
clear
D)
Cannot be determined as the sets A and B are not given done
clear
View Solution play_arrow
-
question_answer42)
Let N be the set of non-negative integers, I the set of integers, \[{{N}_{P}}\] the set of non-positive integers, E the set of even integers and P the set of prime numbers. Then
A)
\[I-N={{N}_{p}}\] done
clear
B)
\[N\cap {{N}_{p}}=\phi \] done
clear
C)
\[E\cap P=\phi \] done
clear
D)
\[N\Delta {{N}_{p}}=I-\{0\}\] done
clear
View Solution play_arrow
-
question_answer43)
Let A and B be two sets then \[(A\cup B)'\cup (A'\cap B)\] is equal to
A)
A? done
clear
B)
A done
clear
C)
B? done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer44)
What does the shaded portion of the Venn diagram given below represent?
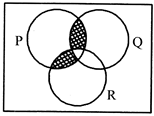
A)
\[(P\cap Q)\cap (P\cap R)\] done
clear
B)
\[((P\cap Q)-R)\cup ((P\cap R)-Q)\] done
clear
C)
\[((P\cup Q)-R)\cap ((P\cap R)-Q)\] done
clear
D)
\[((P\cap Q)\cup R)\cap ((P\cup Q)-R)\] done
clear
View Solution play_arrow
-
question_answer45)
A, B, C and D are four sets such that \[A\cap B=C\cap D=\phi .\] Consider the following:
| 1. \[A\cup B\] and \[B\cup D\] are always disjoint. |
| 2. \[A\cap C\] and \[B\cap D\] are always disjoint. |
| Which of the above statements is/are correct? |
A)
1 Only done
clear
B)
2 only done
clear
C)
Both 1 and 2 done
clear
D)
neither 1 nor 2s done
clear
View Solution play_arrow
-
question_answer46)
Let A, B, C are three non-empty sets. If \[A\subset B\]and \[B\subset C,\]then which of the following is true?
A)
\[B-A=C-B\] done
clear
B)
\[A\cap B\cap C=B\] done
clear
C)
\[A\cup B=B\cap C\] done
clear
D)
\[A\cup B\cup C=A\] done
clear
View Solution play_arrow
-
question_answer47)
Let X and Y be two non-empty sets such that \[X\cap A=Y\cap A=\phi \] and \[X\cup A=Y\cup A\]for some non-empty set A. Then
A)
X is a proper subset of Y done
clear
B)
Y is a proper subset of X done
clear
C)
X = Y done
clear
D)
X and Y are disjoint sets done
clear
View Solution play_arrow
-
question_answer48)
Which one of the following is correct?
A)
\[A\cup P(A)=P(A)(b)\] done
clear
B)
\[A\cap P(A)=A\] done
clear
C)
\[A-P(A)=A\] done
clear
D)
\[P(A)-\{A\}=P(A)\] Here P denotes the power set of a set A. done
clear
View Solution play_arrow
-
question_answer49)
If \[(A-B)\cup (B-A)=A\] for subsets A and B of the universal set U, then which one of the following is correct?
A)
B is proper non-empty subset of A done
clear
B)
A and B are non-empty disjoint sets done
clear
C)
\[B=\phi \] done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer50)
What does the shaded region in the Venn diagram given below represent?
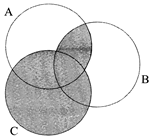
A)
\[C\cap (A'\cap B')\] done
clear
B)
\[C\cup (C'\cap A\cap B)\] done
clear
C)
\[C\cup (C\cap A)\cup (C\cap B)\] done
clear
D)
\[C\cup (A/B)\] done
clear
View Solution play_arrow
-
question_answer51)
Let\[n(U)=700,n(A)=200,n(B)=300,n(A\cap B)=100\]then \[n(A'\cap B')\] is equal to
A)
400 done
clear
B)
600 done
clear
C)
300 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer52)
There are 600 student in a school. If 400 of them can speak Telugu, 300 can speak Hindi, then the number of students who can speak both Telugu and Hindi is:
A)
100 done
clear
B)
200 done
clear
C)
300 done
clear
D)
400 done
clear
View Solution play_arrow
-
question_answer53)
In a group of 50 people, two tests were conducted, one for diabetes and one for blood pressure. 30 people were diagnosed with diabetes and 40 people were diagnosed with high blood pressure. What is the minimum number of people who were having diabetes and high blood pressure?
A)
0 done
clear
B)
10 done
clear
C)
20 done
clear
D)
30 done
clear
View Solution play_arrow
-
question_answer54)
Out of 32 persons, 30 invest in national savings certificates and 17 invest in shares. What is the number of persons who invest in both?
A)
13 done
clear
B)
15 done
clear
C)
17 done
clear
D)
19 done
clear
View Solution play_arrow
-
question_answer55)
Which of the following is correct?
| I. \[n(S\cup T)\] is maximum when n \[n(S\cap T)\] is least, |
| II. If \[n(U)=1000,n(S)=720,n(T)=450,\] then least value of \[n(S\cap T)=170.\] |
A)
Only I is true done
clear
B)
Only II is true done
clear
C)
Both I and II are true done
clear
D)
Both I and II are false done
clear
View Solution play_arrow
-
question_answer56)
In a school, there are 20 teachers who teach mathematics of physics of these, 12 teach mathematics and 4 teach both math?s and physics then the number of teachers teaching only physics are
A)
4 done
clear
B)
8 done
clear
C)
12 done
clear
D)
16 done
clear
View Solution play_arrow
-
question_answer57)
Given \[n(U)=20,n(A)=12,n(B)=9,n(A\cap B)=4,\]where U is the universal set, A and B are subsets of U, then \[n({{(A\cup B)}^{c}})=\]
A)
17 done
clear
B)
9 done
clear
C)
11 done
clear
D)
3 done
clear
View Solution play_arrow
-
question_answer58)
In a town of 10000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy newspaper C, 5% buy A and B, 3% buy B and C and 4% buy A and C. if 2% families buy all of three newspapers, then the number of families which buy A only, is
A)
4400 done
clear
B)
3300 done
clear
C)
2000 done
clear
D)
500 done
clear
View Solution play_arrow
-
question_answer59)
In a class of 30 pupils, 12 take needle work, 16 take physics and 18 take history. If all the 30 students take at least one subject and no one takes all three then the number of pupils taking 2 subjects is
A)
16 done
clear
B)
6 done
clear
C)
8 done
clear
D)
20 done
clear
View Solution play_arrow
-
question_answer60)
Consider the following statements.
| I. If \[{{A}_{n}}\]is the set of first n prime numbers, then \[\underset{n=2}{\overset{10}{\mathop{U}}}\,{{A}_{n}}\]is equal to {2, 3, 5, 7, 11, 13, 17, 19, 23, 29} |
| II. If A and B are two sets such that \[n(A\cup B)=50,\]\[n(A)=28,\,\,n(B)=32,\] then \[n(A\cap B)=10.\] Which of these is correct? |
A)
Only I is true done
clear
B)
Only II is true done
clear
C)
Both are true done
clear
D)
Both are false done
clear
View Solution play_arrow


