question_answer

If \[f(x)=|x-3|,\]then f is [SCRA 1996; RPET 1997]

A)            Discontinuous at \[x=2\]          

B)            Not differentiable \[x=2\]

C)            Differentiable at \[x=3\]          

D)            Continuous but not differentiable at \[x=3\]

Correct Answer: D

Solution :

           \[\underset{x\to {{3}^{-}}}{\mathop{\lim }}\,\,f(x)=\underset{h\to 0}{\mathop{\lim }}\,f(3-h)=\underset{h\to 0}{\mathop{\lim }}\,\,\,|3-h-3|\,\,=0\]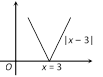            \[\underset{x\to {{3}^{+}}}{\mathop{\lim }}\,\,f(x)=\underset{h\to 0}{\mathop{\lim }}\,f(3+h)=\underset{h\to 0}{\mathop{\lim }}\,\,\,|3+h-3|\,\,=0\]            \[\because \,\,\underset{x\to {{3}^{-}}}{\mathop{\lim }}\,\,f(x)=\underset{x\to {{3}^{+}}}{\mathop{\lim }}\,f(x)=f(3)\]            Hence f is continuous at \[x=3\]            Now  \[L\,{f}'(3)=\underset{h\to 0}{\mathop{\lim }}\,\,\,\frac{f(3-h)-f(3)}{-h}\]                            \[=\underset{h\to 0}{\mathop{\lim }}\,\,\,\frac{|3-h-3|\,\,-0}{-h}=\underset{h\to 0}{\mathop{\lim }}\,\,\frac{h}{-h}=-1\]            \[R\,{f}'(3)=\underset{h\to 0}{\mathop{\lim }}\,\,\,\frac{f(3+h)-f(3)}{h}\]\[=\underset{h\to 0}{\mathop{\lim }}\,\,\,\frac{|3+h-3|\,\,-0}{h}=1\]            \[\because L\,{f}'(3)\,\ne \,R\,{f}'(3)\]. Hence f is not differentiable at \[x=3\].            Trick : Can be seen by graph it is continuous but tangent is not defined at \[x=3\].