question_answer

The function \[f(x)=\left\{ \begin{align}   & x,\,\,\text{if 0}\le x\le \text{1} \\  & \text{1,}\,\text{ if}\,1<x\le 2 \\ \end{align} \right.\] is                                                                              [SCRA 1996]

A)            Continuous at all x, \[0\le x\le 2\]and differentiable at all x, except \[2/3\]in the interval [0,2]

B)            Continuous and differentiable at all x in [0,2]

C)            Not continuous at any point in [0,2]

D)            Not differentiable at any point [0,2]

Correct Answer: A

Solution :

           \[f(x)=\left\{ \begin{array}{*{35}{l}}    x\text{  ,} & 0\le x\le 1  \\    1\text{  ,} & 1<x\le 2  \\ \end{array} \right.\]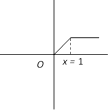            \[\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f(x)=\underset{h\to 0}{\mathop{\lim }}\,f(1-h)\]\[=\underset{h\to 0}{\mathop{\lim }}\,\,\,(1-h)=1\]            \[\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f(x)=\underset{h\to 0}{\mathop{\lim }}\,\,f(1+h)=1\]            Hence function is continuous in (0, 2).            Now \[\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f(x)=\underset{h\to 0}{\mathop{\lim }}\,\,(0+h)=0=f(0)\]            \[\underset{x\to {{2}^{-}}}{\mathop{\lim }}\,f(x)=\underset{h\to 0}{\mathop{\lim }}\,\,(2-h)=1=f(2)\]            Hence function is continuous in [0, 2]                    Clearly, from graph it is not differentiable at \[x=1.\]