A) \[\frac{h\cot q}{\cot q-\cot p}\]
B) \[\frac{h\cot p}{\cot p-\cot q}\]
C) \[\frac{h\tan p}{\tan p-\tan q}\]
D) None of these
Correct Answer: B
Solution :
Let AD be the building of height h and BP be the hill then \[\tan q=\frac{h+x}{y}\] and \[\tan p=\frac{x}{y}\]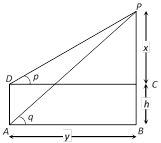 Þ \[\,\tan q=\frac{h+x}{x\cot p}\] \[\Rightarrow \,\,x\cot p=(h+x)\cot q\] Þ \[x=\frac{h\cot q}{\cot p-\cot q}\] Þ \[h+x=\frac{h\cot p}{\cot p-\cot q}\].
Þ \[\,\tan q=\frac{h+x}{x\cot p}\] \[\Rightarrow \,\,x\cot p=(h+x)\cot q\] Þ \[x=\frac{h\cot q}{\cot p-\cot q}\] Þ \[h+x=\frac{h\cot p}{\cot p-\cot q}\].
You need to login to perform this action.
You will be redirected in
3 sec
