A) 62m
B) 301m
C) 101m
D) 75m
E) 52m
Correct Answer: E
Solution :
\[\tan {{30}^{o}}=\frac{h}{x+60}\], \[\frac{1}{\sqrt{3}}=\frac{h}{x+60}\] \[x+60=\sqrt{3}h\], \[x=\sqrt{3}h-60\]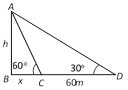 \[\tan {{60}^{o}}=\frac{h}{x}\], \[x=\frac{h}{\sqrt{3}}\] Þ \[\sqrt{3}h-60=\frac{h}{\sqrt{3}}\]Þ \[3h-60\sqrt{3}=h\] Þ \[h=\frac{60\sqrt{3}}{2}=30\sqrt{3}\] \[=51.96\approx 52m\].
\[\tan {{60}^{o}}=\frac{h}{x}\], \[x=\frac{h}{\sqrt{3}}\] Þ \[\sqrt{3}h-60=\frac{h}{\sqrt{3}}\]Þ \[3h-60\sqrt{3}=h\] Þ \[h=\frac{60\sqrt{3}}{2}=30\sqrt{3}\] \[=51.96\approx 52m\].
You need to login to perform this action.
You will be redirected in
3 sec
