-
question_answer1)
For the constraint of a linear optimizing function \[z={{x}_{1}}+{{x}_{2}}\], given by \[{{x}_{1}}+{{x}_{2}}\le 1,\ 3{{x}_{1}}+{{x}_{2}}\ge 3\] and \[{{x}_{1}},\ {{x}_{2}}\ge 0\]
A)
There are two feasible regions done
clear
B)
There are infinite feasible regions done
clear
C)
There is no feasible region done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer2)
Which of the following is not a vertex of the positive region bounded by the inequalities \[2x+3y\le 6\], \[5x+3y\le 15\] and \[x,\ y\ge 0\]
A)
(0, 2) done
clear
B)
(0, 0) done
clear
C)
(3, 0) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer3)
The intermediate solutions of constraints must be checked by substituting them back into
A)
Objective function done
clear
B)
Constraint equations done
clear
C)
Not required done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer4)
For the constraints of a L.P. problem given by \[{{x}_{1}}+2{{x}_{2}}\le 2000\],\[{{x}_{1}}+{{x}_{2}}\le 1500\],\[{{x}_{2}}\le 600\]and \[{{x}_{1}},\ {{x}_{2}}\ge 0\], which one of the following points does not lie in the positive bounded region
A)
(1000, 0) done
clear
B)
(0, 500) done
clear
C)
(2, 0) done
clear
D)
(2000, 0) done
clear
View Solution play_arrow
-
question_answer5)
A basic solution is called non-degenerate, if
A)
All the basic variables are zero done
clear
B)
None of the basic variables is zero done
clear
C)
At least one of the basic variables is zero done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer6)
If the number of available constraints is 3 and the number of parameters to be optimized is 4, then
A)
The objective function can be optimized done
clear
B)
The constraints are short in number done
clear
C)
The solution is problem oriented done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer7)
The solution of set of constraints \[x+2y\ge 11,\] \[3x+4y\le 30,\ \ 2x+5y\le 30,\ x\ge 0,\ \ y\ge 0\] includes the point [MP PET 1993]
A)
(2, 3) done
clear
B)
(3, 2) done
clear
C)
(3, 4) done
clear
D)
(4, 3) done
clear
View Solution play_arrow
-
question_answer8)
The graph of \[x\le 2\] and \[y\ge 2\] will be situated in the
A)
First and second quadrant done
clear
B)
Second and third quadrant done
clear
C)
First and third quadrant done
clear
D)
Third and fourth quadrant done
clear
View Solution play_arrow
-
question_answer9)
The feasible solution of a L.P.P. belongs to
A)
First and second quadrant done
clear
B)
First and third quadrant done
clear
C)
Second quadrant done
clear
D)
Only first quadrant done
clear
View Solution play_arrow
-
question_answer10)
The position of points O (0,0) and P (2, ? 2) in the region of graph of inequation \[2x-3y<5\], will be
A)
O inside and P outside done
clear
B)
O and P both inside done
clear
C)
O and P both outside done
clear
D)
O outside and P inside done
clear
View Solution play_arrow
-
question_answer11)
The true statement for the graph of inequations \[3x+2y\le 6\] and \[6x+4y\ge 20\], is
A)
Both graphs are disjoint done
clear
B)
Both do not contain origin done
clear
C)
Both contain point (1, 1) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer12)
The vertex of common graph of inequalities \[2x+y\ge 2\] and \[x-y\le 3\], is
A)
(0, 0) done
clear
B)
\[\left( \frac{5}{3},\ -\frac{4}{3} \right)\] done
clear
C)
\[\left( \frac{5}{3},\ \frac{4}{3} \right)\] done
clear
D)
\[\left( -\frac{4}{3},\ \frac{5}{3} \right)\] done
clear
View Solution play_arrow
-
question_answer13)
A vertex of bounded region of inequalities \[x\ge 0\], \[x+2y\ge 0\] and \[2x+y\le 4\], is
A)
(1, 1) done
clear
B)
(0, 1) done
clear
C)
(3, 0) done
clear
D)
(0, 0) done
clear
View Solution play_arrow
-
question_answer14)
A vertex of the linear inequalities \[2x+3y\le 6\], \[x+4y\le 4\] and \[x,\ y\ge 0\], is
A)
(1, 0) done
clear
B)
(1, 1) done
clear
C)
\[\left( \frac{12}{5},\ \frac{2}{5} \right)\] done
clear
D)
\[\left( \frac{2}{5},\ \frac{12}{5} \right)\] done
clear
View Solution play_arrow
-
question_answer15)
A vertex of a feasible region by the linear constraints \[3x+4y\le 18,\ 2x+3y\ge 3\] and \[x,\ y\ge 0\], is
A)
(0, 2) done
clear
B)
(4.8, 0) done
clear
C)
(0, 3) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer16)
In which quadrant, the bounded region for inequations \[x+y\le 1\] and \[x-y\le 1\] is situated
A)
I, II done
clear
B)
I, III done
clear
C)
II, III done
clear
D)
All the four quadrants done
clear
View Solution play_arrow
-
question_answer17)
The necessary condition for third quadrant region in xy-plane, is
A)
\[x>0,\ y<0\] done
clear
B)
\[x<0,\ y<0\] done
clear
C)
\[x<0,\ y>0\] done
clear
D)
\[x<0,\ y=0\] done
clear
View Solution play_arrow
-
question_answer18)
For the following feasible region, the linear constraints are
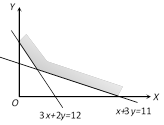
A)
\[x\ge 0,\ y\ge 0,\ 3x+2y\ge 12,\ x+3y\ge 11\] done
clear
B)
\[x\ge 0,\ y\ge 0,\ 3x+2y\le 12,\ x+3y\ge 11\] done
clear
C)
\[x\ge 0,\ y\ge 0,\ 3x+2y\le 12,\ x+3y\le 11\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer19)
The value of objective function is maximum under linear constraints
A)
At the center of feasible region done
clear
B)
At (0, 0) done
clear
C)
At any vertex of feasible region done
clear
D)
The vertex which is at maximum distance from (0, 0) done
clear
View Solution play_arrow
-
question_answer20)
The region represented by \[2x+3y-5\le 0\] and \[4x-3y+2\le 0\], is
A)
Not in first quadrant done
clear
B)
Bounded in first quadrant done
clear
C)
Unbounded in first quadrant done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer21)
The region represented by the inequation system \[x,\ y\ge 0\], \[y\le 6,\ x+y\le 3\], is
A)
Unbounded in first quadrant done
clear
B)
Unbounded in first and second quadrants done
clear
C)
Bounded in first quadrant done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer22)
The solution set of the inequation \[2x+y>5\], is
A)
Half plane that contains the origin done
clear
B)
Open half plane not containing the origin done
clear
C)
Whole xy-plane except the points lying on the line \[2x+y=5\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer23)
If a point (h, k) satisfies an inequation \[ax+by\ge 4\], then the half plane represented by the inequation is
A)
The half plane containing the point (h, k) but excluding the points on \[ax+by=4\] done
clear
B)
The half plane containing the point (h, k) and the points on \[ax+by=4\] done
clear
C)
Whole xy-plane done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer24)
Inequation \[y-x\le 0\] represents
A)
The half plane that contains the positive x-axis done
clear
B)
Closed half plane above the line \[y=x\] which contains positive y-axis done
clear
C)
Half plane that contains the negative x-axis done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer25)
Objective function of a L.P.P. is
A)
A constraint done
clear
B)
A function to be optimized done
clear
C)
A relation between the variables done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer26)
The optimal value of the objective function is attained at the points [MP PET 1998]
A)
Given by intersection of inequations with axes only done
clear
B)
Given by intersection of inequations with x-axis only done
clear
C)
Given by corner points of the feasible region done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer27)
The objective function \[z=4x+3y\] can be maximized subjected to the constraints \[3x+4y\le 24\], \[8x+6y\le 48\], \[x\le 5,\ y\le 6;\ \ x,\ y\ge 0\]
A)
At only one point done
clear
B)
At two points only done
clear
C)
At an infinite number of points done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer28)
If the constraints in a linear programming problem are changed
A)
The problem is to be re-evaluated done
clear
B)
Solution is not defined done
clear
C)
The objective function has to be modified done
clear
D)
The change in constraints is ignored done
clear
View Solution play_arrow
-
question_answer29)
Which of the following statements is correct
A)
Every L.P.P. admits an optimal solution done
clear
B)
A L.P.P. admits a unique optimal solution done
clear
C)
If a L.P.P. admits two optimal solutions, it has an infinite number of optimal solutions done
clear
D)
The set of all feasible solutions of a L.P.P. is not a convex set done
clear
View Solution play_arrow
-
question_answer30)
Shaded region is represented by [MP PET 1997]
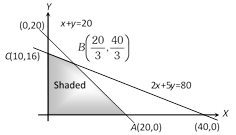
A)
\[2x+5y\ge 80,\ x+y\le 20,\ x\ge 0,\ y\le 0\] done
clear
B)
\[2x+5y\ge 80,\ x+y\ge 20,\ x\ge 0,\ y\ge 0\] done
clear
C)
\[2x+5y\le 80,\ x+y\le 20,\ x\ge 0,\ y\ge 0\] done
clear
D)
\[2x+5y\le 80,\ x+y\le 20,\ x\le 0,\ y\le 0\] done
clear
View Solution play_arrow
-
question_answer31)
The constraints \[-{{x}_{1}}+{{x}_{2}}\le 1\] \[-{{x}_{1}}+3{{x}_{2}}\le 9\] \[{{x}_{1}},\ {{x}_{2}}\ \ge 0\] define on [MP PET 1999]
A)
Bounded feasible space done
clear
B)
Unbounded feasible space done
clear
C)
Both bounded and unbounded feasible space done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer32)
Which of the following is not true for linear programming problems [Kurukshetra CEE 1998]
A)
A slack variable is a variable added to the left hand side of a less than or equal to constraint to convert it into an equality done
clear
B)
A surplus variable is a variable subtracted from the left hand side of a greater than or equal to constraint to convert it into an equality done
clear
C)
A basic solution which is also in the feasible region is called a basic feasible solution done
clear
D)
A column in the simplex tableau that contains all of the variables in the solution is called pivot or key column done
clear
View Solution play_arrow
-
question_answer33)
Which of the terms is not used in a linear programming problem [MP PET 2000]
A)
Slack variables done
clear
B)
Objective function done
clear
C)
Concave region done
clear
D)
Feasible solution done
clear
View Solution play_arrow
-
question_answer34)
The graph of inequations \[x\le y\] and \[y\le x+3\] is located in
A)
II quadrant done
clear
B)
I, II quadrants done
clear
C)
I, II, III quadrants done
clear
D)
II, III, IV quadrants done
clear
View Solution play_arrow
-
question_answer35)
The area of the feasible region for the following constraints \[3y+x\ge 3,\,x\ge 0,\,y\ge 0\] will be [DCE 2005]
A)
Bounded done
clear
B)
Unbounded done
clear
C)
Convex done
clear
D)
Concave done
clear
View Solution play_arrow
-
question_answer36)
The feasible region for the following constraints \[{{L}_{1}}\le 0,{{L}_{2}}\ge 0,\,{{L}_{3}}=0,\,x\ge 0,y\ge 0\] in the diagram shown is
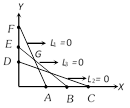
[Kerala (Engg.) 2005]
A)
Area DHF done
clear
B)
Area AHC done
clear
C)
Line segment EG done
clear
D)
Line segment GI done
clear
E)
Line segment IC done
clear
View Solution play_arrow
-
question_answer37)
A wholesale merchant wants to start the business of cereal with Rs. 24000. Wheat is Rs. 400 per quintal and rice is Rs. 600 per quintal. He has capacity to store 200 quintal cereal. He earns the profit Rs. 25 per quintal on wheat and Rs. 40 per quintal on rice. If he stores x quintal rice and y quintal wheat, then for maximum profit the objective function is
A)
\[25x+40y\] done
clear
B)
\[40x+25y\] done
clear
C)
\[400x+600y\] done
clear
D)
\[\frac{400}{40}x+\frac{600}{25}y\] done
clear
View Solution play_arrow
-
question_answer38)
Mohan wants to invest the total amount of Rs. 15,000 in saving certificates and national saving bonds. According to rules, he has to invest at least Rs. 2000 in saving certificates and Rs. 2500 in national saving bonds. The interest rate is 8% on saving certificate and 10% on national saving bonds per annum. He invest Rs. x in saving certificates and Rs. y in national saving bonds. Then the objective function for this problem is
A)
\[0.08x+0.10y\] done
clear
B)
\[\frac{x}{2000}+\frac{y}{2500}\] done
clear
C)
\[2000x+2500y\] done
clear
D)
\[\frac{x}{8}+\frac{y}{10}\] done
clear
View Solution play_arrow
-
question_answer39)
A firm produces two types of products A and B. The profit on both is Rs. 2 per item. Every product requires processing on machines \[{{M}_{1}}\] and \[{{M}_{2}}\]. For A, machines \[{{M}_{1}}\] and \[{{M}_{2}}\] takes 1 minute and 2 minute respectively and for B, machines \[{{M}_{1}}\] and \[{{M}_{2}}\] takes the time 1 minute each. The machines \[{{M}_{1}},\ {{M}_{2}}\] are not available more than 8 hours and 10 hours, any of day, respectively. If the products made x of A and y of B, then the linear constraints for the L.P.P. except \[x\ge 0,\ y\ge 0\], are
A)
\[x+y\le 480\,,\ 2x+y\le 600\] done
clear
B)
\[x+y\le 8,\ 2x+y\le 10\] done
clear
C)
\[x+y\ge 480\,,\ 2x+y\ge 600\] done
clear
D)
\[x+y\le 8,\ 2x+y\ge 10\] done
clear
View Solution play_arrow
-
question_answer40)
The objective function in the above question is
A)
\[2x+y\] done
clear
B)
\[x+2y\] done
clear
C)
\[2x+2y\] done
clear
D)
\[8x+10y\] done
clear
View Solution play_arrow
-
question_answer41)
In a test of Mathematics, there are two types of questions to be answered?short answered and long answered. The relevant data is given below
| Type of questions | Time taken to solve | Marks | Number of questions |
| Short answered questions | 5 minute | 3 | 10 |
| Long answered questions | 10 minute | 5 | 14 |
| | | | |
The total marks is 100. Students can solve all the questions. To secure maximum marks, a student solves x short answered and y long answered questions in three hours, then the linear constraints except\[x\ge 0,\ y\ge 0\], are
A)
\[5x+10y\le 180\], \[x\le 10,\ y\le 14\] done
clear
B)
\[x+10y\ge 180\], \[x\le 10,\ y\le 14\] done
clear
C)
\[5x+10y\ge 180\], \[x\ge 10,\ y\ge 14\] done
clear
D)
\[5x+10y\le 180\], \[x\ge 10,\ y\ge 14\] done
clear
View Solution play_arrow
-
question_answer42)
The objective function for the above question is
A)
\[10x+14y\] done
clear
B)
\[5x+10y\] done
clear
C)
\[3x+5y\] done
clear
D)
\[5y+3x\] done
clear
View Solution play_arrow
-
question_answer43)
The vertices of a feasible region of the above question are
A)
(0, 18), (36, 0) done
clear
B)
(0, 18), (10, 13) done
clear
C)
(10, 13), (8, 14) done
clear
D)
(10, 13), (8, 14), (12, 12) done
clear
View Solution play_arrow
-
question_answer44)
The maximum value of objective function in the above question is
A)
100 done
clear
B)
92 done
clear
C)
95 done
clear
D)
94 done
clear
View Solution play_arrow
-
question_answer45)
A factory produces two products A and B. In the manufacturing of product A, the machine and the carpenter requires 3 hour each and in manufacturing of product B, the machine and carpenter requires 5 hour and 3 hour respectively. The machine and carpenter work at most 80 hour and 50 hour per week respectively. The profit on A and B is Rs. 6 and 8 respectively. If profit is maximum by manufacturing x and y units of A and B type product respectively, then for the function \[6x+8y\] the constraints are
A)
\[x\ge 0,\ y\ge 0,\ 5x+3y\le 80,\ 3x+2y\le 50\] done
clear
B)
\[x\ge 0,\ y\ge 0,\ 3x+5y\le 80,\ 3x+3y\le 50\] done
clear
C)
\[x\ge 0,\ y\ge 0,\ 3x+5y\ge 80,\ 2x+3y\ge 50\] done
clear
D)
\[x\ge 0,\ y\ge 0,\ 5x+3y\ge 80,\ 3x+2y\ge 50\] done
clear
View Solution play_arrow
-
question_answer46)
A shopkeeper wants to purchase two articles A and B of cost price Rs. 4 and 3 respectively. He thought that he may earn 30 paise by selling article A and 10 paise by selling article B. He has not to purchase total article worth more than Rs. 24. If he purchases the number of articles of A and B, x and y respectively, then linear constraints are
A)
\[x\ge 0,\ y\ge 0,\ 4x+3y\le 24\] done
clear
B)
\[x\ge 0,\ y\ge 0,\ 30x+10y\le 24\] done
clear
C)
\[x\ge 0,\ y\ge 0,\ 4x+3y\ge 24\] done
clear
D)
\[x\ge 0,\ y\ge 0,\ 30x+40y\ge 24\] done
clear
View Solution play_arrow
-
question_answer47)
In the above question the is o-profit line is
A)
\[3x+y=30\] done
clear
B)
\[x+3y=20\] done
clear
C)
\[3x-y=20\] done
clear
D)
\[4x+3y=24\] done
clear
View Solution play_arrow
-
question_answer48)
The sum of two positive integers is at most 5. The difference between two times of second number and first number is at most 4. If the first number is x and second number y, then for maximizing the product of these two numbers, the mathematical formulation is
A)
\[x+y\ge 5\], \[2y-x\ge 4,\ \ x\ge 0,\ y\ge 0\] done
clear
B)
\[x+y\ge 5\], \[-2x+y\ge 4,\ \ x\ge 0,\ y\ge 0\] done
clear
C)
\[x+y\le 5\], \[2y-x\le 4,\ \ x\ge 0,\ y\ge 0\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer49)
For the L.P. problem Max\[z=3{{x}_{1}}+2{{x}_{2}}\] such that \[2{{x}_{1}}-{{x}_{2}}\ge 2\], \[{{x}_{1}}+2{{x}_{2}}\le 8\] and \[{{x}_{1}},\ {{x}_{2}}\ge 0\], \[z=\]
A)
12 done
clear
B)
24 done
clear
C)
36 done
clear
D)
40 done
clear
View Solution play_arrow
-
question_answer50)
For the L.P. problem Min\[z=-{{x}_{1}}+2{{x}_{2}}\] such that \[-{{x}_{1}}+3{{x}_{2}}\le 0,\]\[{{x}_{1}}+{{x}_{2}}\le 6,\ {{x}_{1}}-{{x}_{2}}\le 2\]and \[{{x}_{1}},\ {{x}_{2}}\ge 0\],\[{{x}_{1}}=\]
A)
2 done
clear
B)
8 done
clear
C)
10 done
clear
D)
12 done
clear
View Solution play_arrow
-
question_answer51)
For the L.P. problem Min\[z={{x}_{1}}+{{x}_{2}}\] such that \[5{{x}_{1}}+10{{x}_{2}}\le 0,\ \ {{x}_{1}}+{{x}_{2}}\ge 1,\ \ {{x}_{2}}\le 4\] and \[{{x}_{1}},\ {{x}_{2}}\ge 0\]
A)
There is a bounded solution done
clear
B)
There is no solution done
clear
C)
There are infinite solutions done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer52)
On maximizing \[z=4x+9y\] subject to \[x+5y\le 200,\] \[x+5y\le 200,\ \ 2x+3y\le 134\] and \[x,\ y\ge 0\], \[z=\]
A)
380 done
clear
B)
382 done
clear
C)
384 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer53)
For the L.P. problem Min\[z=2x+y\] subject to \[5x+10y\le 50,\] \[x+y\ge 1,\ \ y\le 4\] and \[x,\ y\ge 0\], \[z=\]
A)
0 done
clear
B)
1 done
clear
C)
2 done
clear
D)
½ done
clear
View Solution play_arrow
-
question_answer54)
For the L.P. problem Min\[z=2x-10y\] subject to \[x-y\ge 0,\ \ x-5y\ge -5\] and \[x,\ y\ge 0\], \[z=\]
A)
?10 done
clear
B)
?20 done
clear
C)
0 done
clear
D)
10 done
clear
View Solution play_arrow
-
question_answer55)
The point at which the maximum value of \[(3x+2y)\] subject to the constraints \[x+y\le 2,\ x\ge 0,\ y\ge 0\] is obtained, is [MP PET 1993]
A)
(0, 0) done
clear
B)
(1.5, 1.5) done
clear
C)
(2, 0) done
clear
D)
(0, 2) done
clear
View Solution play_arrow
-
question_answer56)
The minimum value of objective function \[c=2x+2y\] in the given feasible region, is

A)
134 done
clear
B)
40 done
clear
C)
38 done
clear
D)
80 done
clear
View Solution play_arrow
-
question_answer57)
The minimum value of linear objective function \[c=2x+2y\] under linear constraints \[3x+2y\ge 12\], \[x+3y\ge 11\] and \[x,\ y\ge 0\], is
A)
10 done
clear
B)
12 done
clear
C)
6 done
clear
D)
5 done
clear
View Solution play_arrow
-
question_answer58)
The solution for minimizing the function \[z=x+y\] under a L.P.P. with constraints \[x+y\ge 1\], \[x+2y\le 10\], \[y\le 4\] and \[x,\ y\ge 0\], is
A)
\[x=0,\ y=0,\ z=0\] done
clear
B)
\[x=3,\ y=3,\ z=6\] done
clear
C)
There are infinitely solutions done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer59)
The solution of a problem to maximize the objective function \[z=x+2y\] under the constraints \[x-y\le 2\], \[x+y\le 4\] and \[x,\ y\ge 0\], is
A)
\[x=0,\ y=4,\ z=8\] done
clear
B)
\[x=1,\ y=2,\ z=5\] done
clear
C)
\[x=1,\ y=4,\ z=9\] done
clear
D)
\[x=0,\ y=3,\ z=6\] done
clear
View Solution play_arrow
-
question_answer60)
To maximize the objective function \[z=2x+3y\] under the constraints \[x+y\le 30,\ x-y\ge 0,\ y\le 12,\] \[x\le 20,\] \[y\ge 3\] and \[x,\ y\ge 0\]
A)
\[x=12,\ y=18\] done
clear
B)
\[x=18,\ y=12\] done
clear
C)
\[x=12,\ y=12\] done
clear
D)
\[x=20,\ y=10\] done
clear
View Solution play_arrow
-
question_answer61)
The maximum value of \[P=6x+8y\] subject to constraints \[2x+y\le 30,\ x+2y\le 24\] and \[x\ge 0,\ y\ge 0\] is [MP PET 1994; 95]
A)
90 done
clear
B)
120 done
clear
C)
96 done
clear
D)
240 done
clear
View Solution play_arrow
-
question_answer62)
The maximum value of \[P=x+3y\] such that \[2x+y\le 20\], \[x+2y\le 20\], \[x\ge 0,\ y\ge 0\], is [MP PET 1995]
A)
10 done
clear
B)
60 done
clear
C)
30 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer63)
The maximum value of \[z=4x+2y\] subject to the constraints \[2x+3y\le 18,\ x+y\ge 10\]; \[x,\ y\ge 0\], is [MP PET 2001]
A)
36 done
clear
B)
40 done
clear
C)
20 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer64)
\[z=ax+by,\ a,\ b\] being positive, under constraints \[y\ge 1\], \[x-4y+8\ge 0\], \[x,\ y\ge 0\] has
A)
Finite maximum done
clear
B)
Finite minimum done
clear
C)
An unbounded minimum solution done
clear
D)
An unbounded maximum solution done
clear
View Solution play_arrow
-
question_answer65)
By graphical method, the solution of linear programming problem Maximize \[z=3{{x}_{1}}+5{{x}_{2}}\] Subject to \[3{{x}_{1}}+2{{x}_{2}}\le 18\], \[{{x}_{1}}\le 4\], \[{{x}_{2}}\le 6\],\[{{x}_{1}}\ge 0\],\[{{x}_{2}}\ge 0\] is [MP PET 1996]
A)
\[{{x}_{1}}=2,\ {{x}_{2}}=0,\ z=6\] done
clear
B)
\[{{x}_{1}}=2,\ {{x}_{2}}=6,\ z=36\] done
clear
C)
\[{{x}_{1}}=4,\ {{x}_{2}}=3,\ z=27\] done
clear
D)
\[{{x}_{1}}=4,\ {{x}_{2}}=6,\ z=42\] done
clear
View Solution play_arrow
-
question_answer66)
The point at which the maximum value of \[(x+y)\] subject to the constraints \[2x+5y\le 100\], \[\frac{x}{25}+\frac{y}{49}\le 1\], \[x,\ y\ge 0\] is obtained, is
A)
(10, 20) done
clear
B)
(20, 10) done
clear
C)
(15, 15) done
clear
D)
\[\left( \frac{50}{3},\ \frac{40}{3} \right)\] done
clear
View Solution play_arrow
-
question_answer67)
The maximum value of \[(x+2y)\] under the constraints \[2x+3y\le 6,\ x+4y\le 4,\ \ x,\ y\ge 0\] is
A)
3 done
clear
B)
3.2 done
clear
C)
2 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer68)
The maximum value of \[10x+5y\] under the constraints \[3x+y\le 15,\ x+2y\le 8,\] \[x,\ y\ge 0\] is
A)
20 done
clear
B)
50 done
clear
C)
53 done
clear
D)
70 done
clear
View Solution play_arrow
-
question_answer69)
The point at which the maximum value of \[(x+y)\], subject to the constraints \[x+2y\le 70,\ 2x+y\le 95\], \[x,\ y\ge 0\] is obtained, is
A)
(30, 25) done
clear
B)
(20, 35) done
clear
C)
(35, 20) done
clear
D)
(40, 15) done
clear
View Solution play_arrow
-
question_answer70)
If \[3{{x}_{1}}+5{{x}_{2}}\le 15\], \[5{{x}_{1}}+2{{x}_{2}}\le 10\], \[{{x}_{1}},\ {{x}_{2}}\ \ \ge 0\] then the maximum value of \[5{{x}_{1}}+3{{x}_{2}}\], by graphical method is
A)
\[12\frac{7}{19}\] done
clear
B)
\[12\frac{1}{7}\] done
clear
C)
\[12\frac{3}{5}\] done
clear
D)
12 done
clear
View Solution play_arrow
-
question_answer71)
The maximum value of \[z=5x+2y\], subject to the constraints \[x+y\le 7,\ x+2y\le 10\], \[x,\ y\ge 0\] is [AMU 1999]
A)
10 done
clear
B)
26 done
clear
C)
35 done
clear
D)
70 done
clear
View Solution play_arrow
-
question_answer72)
The maximum value of \[z=3x+4y\] subject to the constraints \[x+y\le 40,\ x+2y\le 60,\ x\ge 0\] and \[y\ge 0\] is [MP PET 2002, 04]
A)
120 done
clear
B)
140 done
clear
C)
100 done
clear
D)
160 done
clear
View Solution play_arrow
-
question_answer73)
The minimum value of\[z=2{{x}_{1}}+3{{x}_{2}}\] subject to the constraints\[2{{x}_{1}}+7{{x}_{2}}\ge 22\],\[{{x}_{1}}+{{x}_{2}}\ge 6\],\[5{{x}_{1}}+{{x}_{2}}\ge 10\] and \[{{x}_{1}},\ {{x}_{2}}\ge 0\] is [MP PET 2003]
A)
14 done
clear
B)
20 done
clear
C)
10 done
clear
D)
16 done
clear
View Solution play_arrow
-
question_answer74)
The co-ordinates of the point for minimum value of \[z=7x-8y\]subject to the conditions\[x+y-20\le 0\], \[y\ge 5,\,\] \[x\ge 0\], \[y\ge 0\] is [DCE 2005]
A)
(20, 0) done
clear
B)
(15, 5) done
clear
C)
(0, 5) done
clear
D)
(0, 20) done
clear
View Solution play_arrow
-
question_answer75)
The maximum value of \[\mu =3x+4y\], subject to the conditions \[x+y\le 40,x+2y\le 60,x,y\ge 0\] is [MP PET 2004]
A)
130 done
clear
B)
120 done
clear
C)
40 done
clear
D)
140 done
clear
View Solution play_arrow


