question_answer

If in a right-angled \[\Delta ACB,\] \[\tan \,B=\frac{12}{5},\] then \[\sin B\] is:           (CBSE 2014)

A) \[\frac{12}{13}\]

B) \[\frac{5}{13}\]

C) \[\frac{7}{13}\]

D) \[\frac{9}{13}\]

Correct Answer: A

Solution :

[a] Given,

\[\tan B=\frac{12}{5}=\frac{P}{B}\]

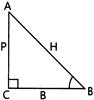Let\[P=12K\]

and \[B=5K\]

Now, in right-angled \[\Delta ABC,\]

\[{{H}^{2}}={{P}^{2}}+{{B}^{2}}\] (By Pythagoras theorem)

\[\Rightarrow \,\,\,\,\,{{H}^{2}}={{(12K)}^{2}}+{{(5K)}^{2}}=144{{K}^{2}}+25{{K}^{2}}=169{{K}^{2}}\]

\[\Rightarrow \,\,\,\,\,H=13K\]

\[\therefore \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sin B=\frac{P}{H}=\frac{12K}{13K}=\frac{12}{13}\]