question_answer

If \[\tan \theta =\frac{3}{4},\]then \[{{\cos }^{2}}\theta -{{\sin }^{2}}\theta =\]

A) \[\frac{7}{25}\]

B) \[1\]

C) \[\frac{-7}{25}\]

D) \[\frac{4}{25}\]

Correct Answer: A

Solution :

[a] We have,  \[\tan \theta =\frac{AB}{BC}=\frac{3}{4}\]

Let \[AB=3k,\] \[BC=4k,\]where k is positive constant.

\[\therefore \,\,\,\,\,\,A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]

\[\Rightarrow \,\,\,A{{C}^{2}}=9{{k}^{2}}+16{{k}^{2}}=25{{k}^{2}}\]

\[\Rightarrow \,\,\,AC=5k\]

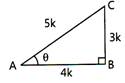\[\therefore \,\,\,\,\,\cos \theta =\frac{BC}{AC}=\frac{4k}{5k}=\frac{4}{5}\]

and \[\sin \theta =\frac{AB}{AC}=\frac{3k}{5k}=\frac{3}{5}\]

\[\therefore \,\,\,\,{{\cos }^{2}}\theta -{{\sin }^{2}}\theta ={{\left( \frac{4}{5} \right)}^{2}}-{{\left( \frac{3}{5} \right)}^{2}}=\frac{16}{25}-\frac{9}{25}=\frac{7}{25}\]