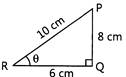
| From the figurer, the value of \[25({{\sin }^{2}}\theta +2{{\cos }^{2}}\theta -\tan \theta )\] is |
 |
A) \[\frac{2}{3}\]
B) \[-\frac{2}{3}\]
C) \[\frac{3}{2}\]
D) \[-\frac{3}{2}\]
Correct Answer: A
Solution :
| [a] From the figure, we have |
| \[\sin \theta =\frac{PQ}{PR}=\frac{8}{10}=\frac{4}{5};\] \[\cos \theta =\frac{QR}{PR}=\frac{6}{10}=\frac{3}{5}\] |
| \[\tan \theta =\frac{PQ}{QR}=\frac{8}{6}=\frac{4}{3}\] |
| \[\therefore \,\,25({{\sin }^{2}}\theta +2{{\cos }^{2}}\theta -\tan \theta )=25\left( \frac{16}{25}+2\times \frac{9}{25}-\frac{4}{3} \right)\]\[=25\left( \frac{48+54-100}{25\times 3} \right)=\frac{2}{3}\] |
You need to login to perform this action.
You will be redirected in
3 sec
