question_answer

The area of the closed figure bounded \[y=\frac{{{x}^{2}}}{2}-2x+2\] and the tangents to it at (1, 1/2) and (4, 2) is

A) 9/8 sq. units      

B) 3/8 sq. units

C) 3/2 sq. units      

D) 9/4 sq. units

Correct Answer: A

Solution :

[a] \[y=\frac{{{x}^{2}}}{2}-2x+2=\frac{{{(x-2)}^{2}}}{2},\] \[\frac{dy}{dx}=x-2,\] \[{{\left( \frac{dy}{dx} \right)}_{x=1}}=-1,\]\[{{\left( \frac{dy}{dx} \right)}_{x=4}}=2,\] Thus, tangent at (1, 1/2) is \[y-1/2=-1(x-1)\]or \[2x+2y-3=0\] Tangent at \[(4,2)\] is \[y-2=2(x-4)\] or \[2x-y-6=0\]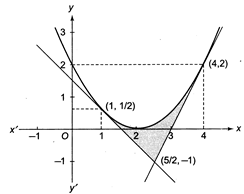 Hence, \[A=\int\limits_{1}^{5/2}{\left( \frac{{{x}^{2}}}{2}-2x+2-\frac{3-2x}{2} \right)dx}\]\[+\int\limits_{5/2}^{4}{\left( \frac{{{x}^{2}}}{2}-2x+2-(2x-6) \right)dx}\] \[=\int\limits_{1}^{4}{\left( \frac{{{x}^{2}}}{2}-2x+2 \right)dx-\int\limits_{1}^{5/2}{\left( \frac{3-2x}{2} \right)dx}}\] \[-\int\limits_{5/2}^{4}{(2x-6)dx}\] \[={{\left( \frac{{{x}^{3}}}{6}-{{x}^{2}}+2x \right)}_{1}}^{4}-\frac{1}{2}{{(3x-{{x}^{2}})}_{1}}^{5/2}-\left( {{x}^{2}}-6x \right)_{5/2}^{4}\]

\[=\left( \frac{63}{6}-15+6 \right)-\frac{1}{2}\left( 3\times \frac{3}{2}-\left( \frac{25}{4}-1 \right) \right)-\left( \left( 16-\frac{25}{4} \right)-6\left( 4-\frac{5}{2} \right) \right)\]

\[=\frac{3}{2}-\frac{1}{2}\left( \frac{9}{2}-\frac{21}{4} \right)-\left( \frac{39}{4}-6\left( \frac{3}{2} \right) \right)\]

\[=\frac{9}{8}sq.units\]