question_answer

The area bounded by the curve \[{{y}^{2}}(2-x)={{x}^{3}}\] and x = 2 is

A) \[\frac{\pi }{2}\]            

B) \[\pi \]

C) \[2\pi \] 

D) \[3\pi \]

Correct Answer: D

Solution :

[d] \[{{y}^{2}}(2-x)={{x}^{3}}\] \[\therefore {{y}^{2}}=\frac{{{x}^{3}}}{2-x}\] \[\therefore y=\pm \frac{{{x}^{3/2}}}{\sqrt{2-x}}\] Clearly, \[x\in \left[ 0,2 \right)\] Consider \[y=\frac{{{x}^{3/2}}}{\sqrt{2-x}}\] When x=0, then y=0. Also, when x increases from 0 to 2, y increases from 0 to\[\infty \]. Hence, graph of given relation is as shown in the following figure: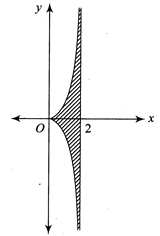 Required Area, \[A=2\int\limits_{0}^{2}{\frac{{{x}^{3/2}}}{\sqrt{2-x}}dx}\] Putting \[x=2{{\sin }^{2}}\theta ,\] we get \[A=2\int\limits_{0}^{\pi /2}{\frac{2\sqrt{2}{{\sin }^{3}}\theta }{\sqrt{2-2{{\sin }^{2}}\theta }}4\sin \theta \cos \theta \,d\theta }\] \[=16\int\limits_{0}^{\pi /2}{{{\sin }^{4}}\theta \,d\theta =16\int\limits_{0}^{\pi /2}{\frac{{{(1-cos2\theta )}^{2}}}{4}}d\theta }\] \[=4\int\limits_{0}^{\pi /2}{(1-2cos2\theta +co{{s}^{2}}2\theta )d\theta }\] \[=4\int\limits_{0}^{\pi /2}{\left( 1-2\cos 2\theta +\frac{1+\cos 4\theta }{2} \right)d\theta }\] \[=4{{\left( \theta +\sin 2\theta +\frac{\theta +\frac{\sin 4\theta }{4}}{2} \right)}_{0}}^{\pi /2}\] \[=4\left( \frac{\pi }{2}+0+\frac{\pi }{4} \right)\] \[=3\pi \]