A) \[\frac{\pi }{2}<l<\frac{{{\pi }^{2}}}{4}\]
B) \[\frac{\pi }{4}<l<\frac{{{\pi }^{2}}}{2}\]
C) \[1<l<\frac{\pi }{2}\]
D) \[0<l<1\]
Correct Answer: A
Solution :
[a] \[\sin x\frac{dy}{dx}+y\cos x=1\] \[\frac{dy}{dx}+y\cot x=\cos ecx\] IF \[={{e}^{\int{\cot xdx}}}={{e}^{ln(sinx)}}=\sin x\] \[y\sin x=\int{\cos ecx.\sin xdx=x+C}\] IF \[x=0,y\] is finite \[\therefore C=0\] \[y=x(cosec\,x)=\frac{x}{\sin \,\,x}\] Now, \[l<\frac{{{\pi }^{2}}}{4}andl>\frac{\pi }{2}\] Hence, \[\frac{\pi }{2}<l<\frac{{{\pi }^{2}}}{4}\]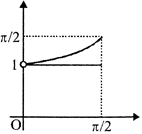
You need to login to perform this action.
You will be redirected in
3 sec
