question_answer

A curve is such that the portion of the x-axis cut off between the origin and the tangent at a point is twice the abscissa and which passes through the point (1, 2). The equation of the curve is

A) \[xy=1\]

B) \[xy=2\]

C) \[xy=3\]

D) None of these

Correct Answer: B

Solution :

[b]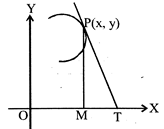  Let P(x, y) be any point on the curve, PM the perpendicular to x-axis PT the tangent at P meeting the axis of x at T. as given OT=2 OM=2x. equation of the tangent at P(x, y) is \[Y-y=\frac{dy}{dx}(X-x)\] It intersects the axis of x where Y=0 i.e \[-y=\frac{dy}{dx}(X-x)\] or \[X=x-y\frac{dy}{dx}=OT\] Hence \[x-y\frac{dy}{dx}=2x\] or \[\frac{dx}{x}+\frac{dy}{y}=0\] Integrating, \[\log x+\log y=\log \,C\] i.e., xy=C. This passes through (1, 2) \[\therefore C=2.\] Hence the required curve is xy = 2