question_answer

                          The maximum value of \[z=3x+2y,\]subjected to the conditions \[x+2y\ge 2,x+2y\le 8,x,y\ge 0\] is

A) 32

B) 24

C) 40

D) None of these

Correct Answer: B

Solution :

[b] Given: \[x+2y\]         \[\ge 2\] (1)

\[x+2y\]                                    \[\le 8\]  (2)

And \[x,y\]                     \[\ge 0\]

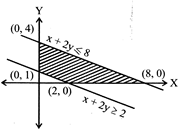For equation (1) \[\frac{x}{2}+\frac{y}{1}=1\] and for equation

(2) \[\frac{x}{8}+\frac{y}{4}=1\]

Given: \[z=3x+2y\]

At point \[(2,0);z=3\times 2+0=6\]

At point \[(0,1);z=3\times 0+2\times 1=2\]

At point \[(8,0);z=3\times 8+2\times 0=24\]

At point \[(0,4);z=3\times 0+2\times 4=8\]

\[\therefore \] Maximum value of z is 24 at point (8, 0).