question_answer

\[Z=7x+y,\] subject to\[5x+y\ge 5,x+y\ge 3,x\ge 0,y\ge 0.\] The minimum value of Z occurs at

A) (3, 0)

B) \[\left( \frac{1}{2},\frac{5}{2} \right)\]

C) (7, 0)

D) (0, 5)

Correct Answer: D

Solution :

[d] We have, maximize \[Z=7x+y.\] subject to:

\[5x+y\ge 5,x+y\ge 3,x,y\ge 0.\]

Let \[{{\ell }_{1}}:5x+y=5\]

\[{{\ell }_{2}}:x+y=3\]

\[{{\ell }_{3}}:x=0\] and \[{{\ell }_{4}}:y=0\]

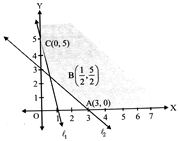
Shaded portion is the feasible region,

Where \[A(3,0),B\left( \frac{1}{2},\frac{5}{2} \right),C(0,5)\]

For B: solving \[{{\ell }_{1}}\] and\[{{\ell }_{2}}\], we get \[B\left( \frac{1}{2},\frac{5}{2} \right)\]

Now maximize \[Z=7x+y\]

Z at B \[\left( \frac{1}{2},\frac{5}{2} \right)=7\left( \frac{1}{2} \right)+\frac{5}{2}=6\]

Z at C (0, 5) =7(0) +5=5

Thus Z, is minimized at C (0, 5) and its minimum value is 5