question_answer

A regular polygon with equal sides has 9 diagonals. Two of the vertices are at \[A(-1,0)\] and\[B(1,0)\]. Possible areas of polygon is

A) \[\frac{3\sqrt{3}}{2},2\sqrt{3},6\sqrt{3}\]

B) \[2\sqrt{3},3\sqrt{3},6\sqrt{3}\]

C) \[9\sqrt{3},6\sqrt{3},2\sqrt{3}\]

D) \[\frac{3\sqrt{3}}{2},3\sqrt{3},6\sqrt{3}\]

Correct Answer: A

Solution :

[a] If polygon has n sides, then the number of diagonals

\[=\frac{n(n-3)}{2}=9\]

\[\therefore n=6\]

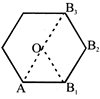Now A and B can be adjacent vertices atternate vertices or opposite vertices

If A and B are adjacent then side \[AB=2,\] then

\[area=6\times \Delta OAB\]

i.e. area \[=6\times \frac{\sqrt{3}}{4}\times {{(2)}^{2}}=6\sqrt{3}\]

If A and B are alternate, then

\[2\cos 30{}^\circ =a+a\cos 60{}^\circ \]

\[\therefore \] Side \[a=\frac{2}{\sqrt{3}}\]

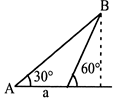\[\therefore \] Area \[=6\times \frac{\sqrt{3}}{4}{{\left( \frac{2}{\sqrt{3}} \right)}^{2}}=2\sqrt{3}\]

Finally if A and B are opposite vertices then side

\[a=\frac{1}{2}AB=1\]

Then area \[=6\times \frac{\sqrt{3}}{4}{{(1)}^{2}}=\frac{3\sqrt{3}}{2}\]