question_answer

Locus of midpoint of the portion between the axes of \[x\cos \alpha +y\sin \alpha =p\] where p is constant is

A) \[{{x}^{2}}+{{y}^{2}}=\frac{4}{{{p}^{2}}}\]

B) \[{{x}^{2}}+{{y}^{2}}=4{{p}^{2}}\]

C) \[\frac{1}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}=\frac{2}{{{p}^{2}}}\]

D) \[\frac{1}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}=\frac{4}{{{p}^{2}}}\]  

Correct Answer: D

Solution :

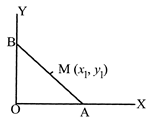
[d] Equation of AB is

\[x\cos \alpha +y\sin \alpha =p;\]

\[\Rightarrow \frac{x\cos \alpha }{p}+\frac{y\sin \alpha }{p}=1;\]

\[\Rightarrow \frac{x}{p/\cos \alpha }+\frac{y}{p/\sin \alpha }=1\]

So co-ordinates of A and B are

\[\left( \frac{p}{\cos \,\alpha },0 \right)\] and \[\left( 0,\frac{p}{\sin \alpha } \right)\];

So co-ordinates of midpoint of AB are

\[\left( \frac{p}{2\cos \alpha },\frac{p}{2\sin \alpha } \right)=({{x}_{1}},{{y}_{1}})(say);\]

\[{{x}_{1}}=\frac{p}{2\cos \alpha }\And {{y}_{1}}=\frac{p}{2\sin \alpha };\]

\[\Rightarrow \cos \alpha =p/2{{x}_{1}}\] and \[\sin \alpha =p/2{{y}_{1}};\]

Consider \[{{\cos }^{2}}\alpha +{{\sin }^{2}}\alpha =1\]

\[\Rightarrow \frac{{{p}^{2}}}{4}\left( \frac{1}{{{x}_{1}}^{2}}+\frac{1}{{{y}^{2}}_{1}} \right)=1\]

\[\therefore \] Locus of \[({{x}_{1}},{{y}_{1}})\] is \[\frac{1}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}=\frac{4}{{{p}^{2}}}.\]