question_answer

The point \[A(2,1)\] is translated parallel to the line \[x-y=3\] by, a distance of 4 units. If the new position A? is in the third quadrant, then the coordinates of A? are

A) \[(2+2\sqrt{2},1+2\sqrt{2})\]

B) \[(-2+\sqrt{2},-1-2\sqrt{2})\]

C) \[(2-2\sqrt{2},1-2\sqrt{2})\]

D) None of these

Correct Answer: C

Solution :

[c] Since the point A(2, 1) is translated parallel to \[x-y=3,\] AA? has the same slope as that of \[x-y=3.\]Therefore, AA? passes through (2, 1) and has slope 1. Here, \[\tan \theta =1\] or

Thus, the equation of AA? is

\[\cos \theta =1/\sqrt{2},\sin \theta =1/\sqrt{2}\]

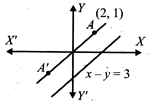Thus, the equation of AA? is

\[\frac{x-2}{\cos (\pi /4)}=\frac{y-1}{\sin (\pi /4)}\]

Since AA?=4, the coordinates of A? are given by

\[\frac{x-2}{\cos (\pi /4)}=\frac{y-1}{\sin (\pi /4)}=-4\]

or \[x=2-4\cos \frac{\pi }{4},y=1-4\sin \frac{\pi }{4}\]

or \[x=2-2\sqrt{2},y=1-2\sqrt{2}\]

Hence, the coordinates of A? are

\[(2-2\sqrt{2},1-2\sqrt{2}).\]